基于Go语言实现插入排序算法及优化

目录

• 插入排序
• 算法实现
• 算法优化
• 小结

插入排序

插入排序是一种简单的排序算法，以数组为例，我们可以把数组看成是多个数组组成。插入排序的基本思想是往前面已排好序的数组中插入一个元素，组成一个新的数组，此数组依然有序。光看文字可能不理解，让我们看看图示：

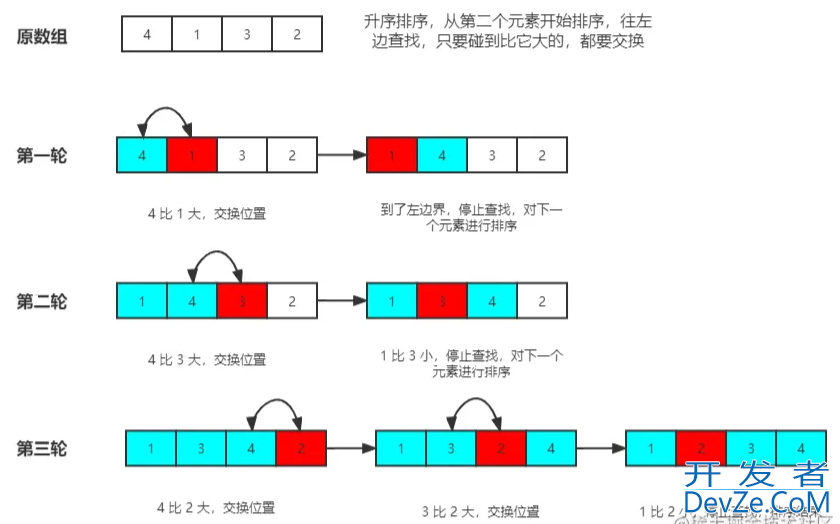
插入排序的时间复杂度为 O(N²)。

算法实现

import (
    "fmt"
)

func main() {
    nums := [4]int{4, 1, 3, 2}
    fmt.phpPrintln("原数组：", nums)
    fmt.Println("--------------------------------")
    InsertionSort(nums)
}

func InsertionSort(nums [4]int) {
    for i := 1; i < len(nums); i++ {
            for j := i; j > 0 && 编程客栈nums[j] < nums[j-1]; j-- {
  python                  nums[j], nums[j-1] = nums[j-1], nums[j]
            }
            fmt.Printf("第 %d 轮后：%v\n", i, nums)
    }
    fmt.Println("--------------------------------")
    fmt.Println("排序后的数组：", nums)
}

执行结果：

原数组： [4 1 3 2]

--------------------------------

第 1 轮后：[1 4 3 2]

第 2 轮后：[1 3 4 2]

第 3 轮后：[1 2 3 4]

------------------------------android--

排序后的数组： [1 2 3 4]

1.第一层循环的 i 变量，表示待排序的元素；

2.第二层循环：

j 变量的初值为 i 的值，由 j 变量往前去寻找待插入的位置；

• 循环条件为 j > 0 && nums[j] < nums[j - 1]：
• j > 0 &rarrhttp://www.devze.com; 寻找到左边界则结束寻找；

nums[j] < nums[j - 1] → 左边元素小于待排序的元素则结束寻找;

3.循环体为元素交换逻辑，只要满足循环条件，则不断交换元素，直到交换到待插入的位置，才终止。

算法优化

上面的代码，是通过不断地交换元素，直到无法交换，才能将元素放置到待插入的位置，为了避免频繁交换元素而导致效率低，将交换的逻辑变成把前面的数往后移，最后再将待排序的元素插入到合适的位置即可。

import (
    "fmt"
)

func main() {
    nums := [4]int{4, 1, 3, 2}
    fmt.Println("原数组：", nums)
    fmt.Println("--------------------------------")
    InsertionSort(nums)
}

func InsertionSort(nums [4]int) {
    for i := 1; i < len(nums); i++ {
        t := nums[i]
        j := i
        for ; j > 0 && t < nums[j-1]; j-- {
            nums[j] = nums[j-1]
        }
        nums[j] = t
        fmt.Printf("第 %d 轮后：%v\n", i, nums)
    }
    fmt.Println("--------------------------------")
    fmt.Println("排序后的数组：", nums)
}

用变量 t 记录待排序的元素，用 j 变量往前查找，只要前面的数比 t 大，那么就往后移，最开发者_开发教程后将 t 插入到合适的位置。

小结

本文首先对插入排序进行简单地介绍，通过图片来演示插入排序的过程，然后使用 Go 语言实现插入排序的算法。为减少算法中交换次数的逻辑，对算法进行优化，将交换的逻辑变成把前面的数往后移，最后将待排序的数插入到合适的位置即可。

除了这种优化方式，还有一种改造方式：普通的算法往左查找的方式是线性查找，由于元素是有序的，因此线性查找可以换成二分查找，但是经过二分找到待插入的位置之后，也得移动前面的元素，相比上面的优化方法，还多了 O(logn) 的查找时间复杂度，因此我认为没有必要改造成二分查找。

到此这篇关于基于Go语言实现插入排序算法及优化的文章就介绍到这了,更多相关Go语言插入排序算法内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！