HashMap中哈希值与数组坐标的关联方式

目录

• 1、哈希值的生成与处理
• 2、计算桶的索引
• 3、哈希值总结
• 4、哈希冲突解决方案
• 4.1. 拉链法（Separate Chaining）
• 4.2. 开放寻址法（Open Addressiphpng）
• 1、线性探测（Linear Probing）
• 2、二次探测（Quadratic Probing）
• 3、双重哈希（Double Hashing）
• 总结

在 HashMap 中，通过对键的哈希值进行处理，能够将生成的哈希码映射到 HashMap 内部数组（桶）中的索引位置。

如下图所示：

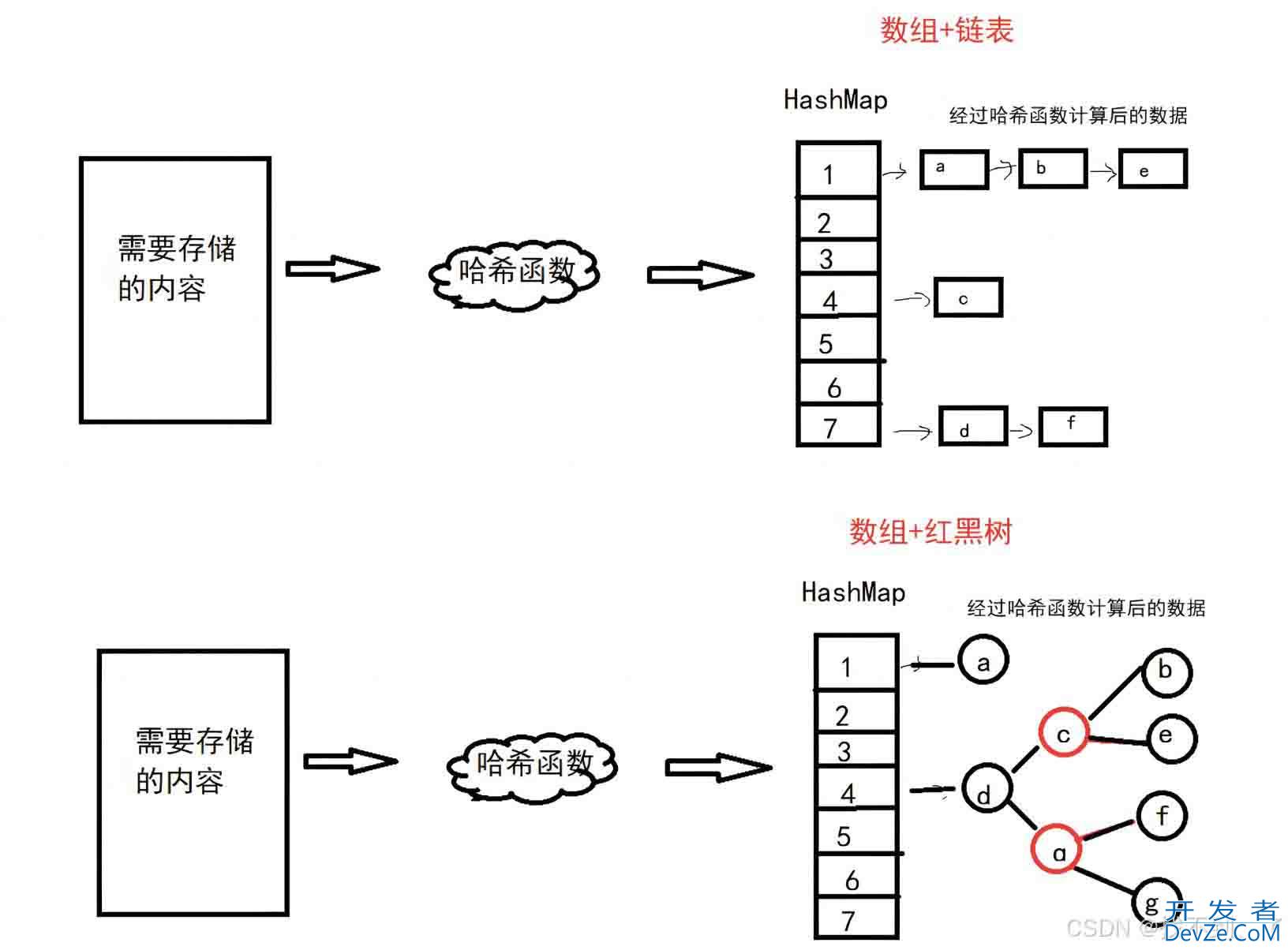
这一过程可以通过以下步骤认真分析：

想了解更多map数据结构更多的可参考：HashMap的扩容机制

1、哈希值的生成与处理

如我们之前讨论的，第一次会调用 hashCode() 方法来生成一个完整的 32 位整数哈希码。然后，使用以下代码对哈希值进行处理：

int h = key.hashCode();
h ^= (h >>> 16python);

2、计算桶的索引

经过处理后，哈希值可能会更分散，最后会用于计算桶的索引位置：

int index = h & (n - 1);

2.1 这里的计算方法：

• n 是当前 HashMap 内部数组的长度（即桶的数量）。为了更高效地计算数组索引，我们通常选择 n 为 2 的幂（例如 16、32、64 等），这允许高效的位操作。
• n - 1 的计算是为了确保采用位与运算来进行取模操作。例如，如果 n 为 16（即 10000），那么 n - 1 为 15（即 01111）。这样做的好处是通过位与运算能够快速计算出在数组中的有效索引。

2.2 示例

假设生成的哈希值 h 为 0b11010110110101101010011000111101（即 32 位二进制数），并且 HashMap 的桶数量 n 为 16（也即 index = h & 15）。

计算过程：

• 二进制示例哈希值：11010110110101101010011000111101
• n-1：00000000000000000000000000001111 （编程即 15 的二进制表示）

进行位与操作：

        11010110110101101010011000111101
  &     000000000php00000000000000000001111
  ------------------------------------------
        00000000000000000000000000000101  （结果即为 index）

• 结果 index 是 5，表示该键值对应的元素存放在 HashMap 的第 5 个桶（数组索引为 5 的位置）。

3、哈希值总结

• 哈希值处理：通过对原始哈希码的处理（即与高位信息进行异或），可以确保更均匀的哈希分布，从而减少碰撞的机会。
• 桶的索引计算：使用 h & (n - 1) 技巧使得计算过程高效，将生成的哈希值直接映射到 HashMap 内部数组的有效索引，从而实现快速的键值对存储和检索。
• 效率：以上步骤都是为了确保在 O(1) 平均情况下能快速访问 HashMap 中的元素，同时减少由于哈希冲突引起的性能损失。

4、哈希冲突解决方案

拉链法（Separate Chaining）和开放寻址法（Open Addressing）是两种常用的哈希表冲突解决策略。

它们在处理两个或多个键冲突（即哈希函数返回相同索引）时采取不同的策略。

下面是对这两种方法的详细介绍及示例：

4.1. 拉链法（编程客栈Separate Chaining）

1.原理

基本思路是为每个哈希表的桶（数组索引）维护一个链表（或其他数据结构），用来存储所有哈希到同一索引位置的键值对。当发生冲突时，新的键值对会被追加到这个链表中。

2.特点

• 冲突分离：拉链法可以有效处理冲突，因为每个桶可以容纳多个元素。
• 空间利用率：空间利用率较高，尤其在负载因子较大时。

3.示例

设想一个简单的哈希表，哈希函数为 h(key) = key mod 5，并且存在以下键值对：

• (3, "A")
• (8, "B")
• (13, "C")
• (9, "D")

哈希表的桶数组将如下所示（使用链表处理冲突）：

Index: 0  -> null
Index: 1  -> null
Index: 2  -> null
Index: 3  -> (3, "A") -> null
Index: 4  -> (8, "B") -> null

当插入键 13，计算得到 h(13) = 3，这个键会追加到索引 3 的链表中：

Index: 0  -> null
Index: 1  -> null
Index: 2  -> null
Index: 3  -> (3, "A") -> (13, "C") -> null
Index: 4  -> (8, "B") -> null

4.2. 开放寻址法（Open Addressing）

1.原理

开放寻址法在发生哈希冲突时，会在哈希表的数组中寻找下一个可用的桶来存储冲突的元素。

常用的方法包括线性探测、二次探测和双重哈希等。

2.特点

• 使用数组存储数据：所有数据都存储在哈希表的原始数组中，不需要额外的链表或其他数据结构。
• 查找时间：在平均情况下，查找时间复杂度与负载因子密切相关，负载因子过高可能导致性能下降。

3.示例

仍然使用相同的哈希函数 h(key) = key mod 5，并且存在以下键值对：

• (3, "A")
• (8, "B")
• (9, "D")

假设当前哈希表的索引结构如下：

Index: 0  -> null
Index: 1  -> null
Index: 2  -> null
Index: 3  -> (3, "A") 
Index: 4  -> (8, "B") 

当插入键 9 时，计算得到 h(9) = 4，但索引 4 已经被占用，因此会采取开放寻址法策略查找下一个可用位置。这个位置是索引 0（线性探测），最终得到如下数据结构：

Index: 0  -> (9, "D")
Index: 1  -> null
Index: 2  -> null
Index: 3  -> (3, "A") 
Index: 4  -> (8, "B") 

常用的探测方法

1、线性探测（Linear Probing）

• 当发生冲突时，逐个检查下一个可用的桶。通过简单地向后移动（对当前索引加 1）来查找下一个位置。
• 例如，如果索引 ii 已经被占用，就检查 (i+1)(i+1)， (i+2)(i+2)，...直到找到空桶。

这种方法的实现如下：

public int linearProbe(int hash, int i) {
    return (hash + i) % table.length;
}

2、二次探测（Quadratic Probing）

• 对于每次冲突，使用二次函数（例如，i2i2）的方式查找下一个位置。这有助于减少碰撞和聚集问题。
• 例如，如果索引 ii 已经被占用，就检查 (i+12)(i+12)，(i+22)(i+22)，(i+32)(i+32)，...直到找到空桶。

实现类似于：

public int quadraticProbe(int hash, int i) {
    return (hash + i * i) % table.length;
}

3、双重哈希（Double Hashing）

• 两个不同的哈希函数同时使用，第一次利用主哈希函数获取初步的索引，若发生冲突，则根据第二个哈希函数计算步长。这种方法能够减小聚集问题。
• 例如，如果主哈希函数返回的索引 h1h1，而第二个哈希函数返回 h2h2，那么如果发生冲突，查找下一个位置的方法为：

public int doubleHash(int hash, int i) {
    return (hash + i * secondHash(key)) % table.length;
}

心得

在开放寻址法中，探测的基础是通过某种方式计算下一个桶的索引，从而避免冲突并正确处理数据。

每种探测方法（线性、二次、双重）各有优缺点，实际使用时可以根据应用需求、性能和负载因子来选择合适的探测方式。

总结

以上为个人经验，希望能给大家一个参考，也希望大家多多支持编程客栈(www.devze.com)。