如何使用Python程序完成描述性统计分析需求

目录

• 一、前言
• 1.1 关于描述性统计分析
• 1.2 本篇目的
• 1.3 提示
• 二、程序内容的编写
• 2.1 导入数据与前期处理
•  2.2 描述性统计分析所要计算的数据
• 2.3 数据可视化
• 2.3.1 概述
• 2.3.2 思路
• 2.4 补充内容
• 三、完整代码与总结

一、前言

1.1 关于描述性统计分析

概括地来说，描述性统计分析就是在收集到的数据的基础上，运用制表和分类，图形以及计算概括性数据来描述数据特征的各项活动。重要的是，该方法主要内容包括频数分析、集中趋势分析、离散程度分析、分布以及一些基本的统计图形。

1.2 本篇目的

本篇内容主要是编写python代码，以实现描述性统计的基本需求，即通过程序获得在描述性统计分析时所需要的数据内容。具体见下。

1.3 提示

本系列篇属于实践类型的代码编写，需要一定的代码基础，因此有不理解的函数或方法可以查找他人的教程或是看本人所写的基础篇分享。本篇的中心内容是2.1与2.2部分，该部分代码可直接使用，根据需要可自行修改；而2.3可视化部分了解思路与代码框架即可，代码可根据个人需要重写。

二、程序内容的编写

2.1 导入数据与前期处理

首先是导入excel表格里的数据，并进行一些基本的设置。

import pandas apythons pd
import numpy as np
import matplotlib.pyplot as plt
pd.set_option('display.max_columns',1000)
pd.set_option("display.width",1000)
pd.set_option('display.max_colwidth',1000)
pd.set_option('display.max_rows',1000)#将行和列的最大展示值设置到1000，则可展示更多的行而不是以省略号形式展示。
df=pd.read_excel(r'D:\杂货\编码数据.xlsx',sheet_name='编码数据')

第一、二、三行分别是导入pandas,numpy,matplotlib库，后面会用到库的内容来编写。

第四到第七行分别是将导入列表的输出展示内容扩大到1000的数量（按照需要，1000这个数值还可以设置的更大），这样在打印输出表格的时候，就不会出现省略号省略掉中间内容的情况。就像我在第一篇基础篇中导入excel时出现的情况：

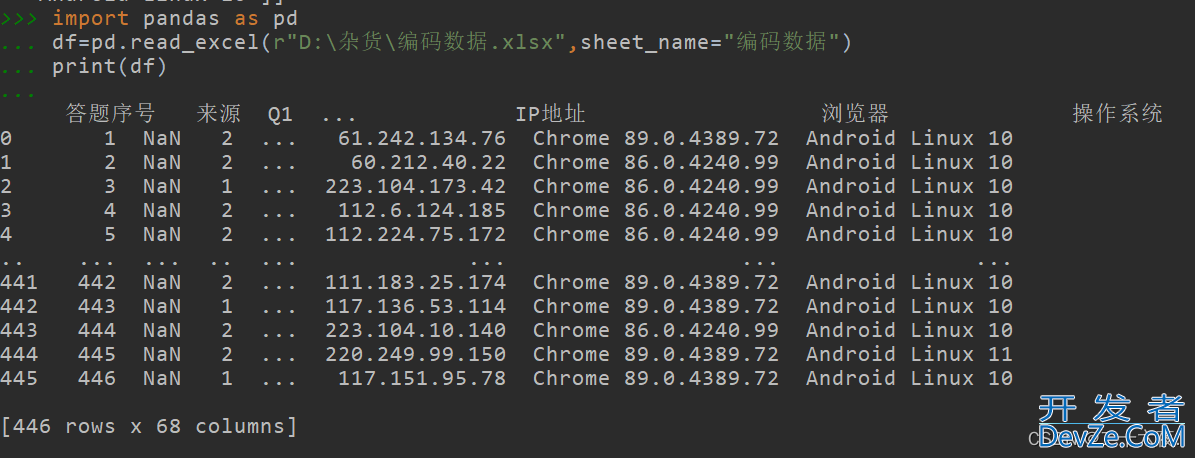
 设置好后的输出情况：

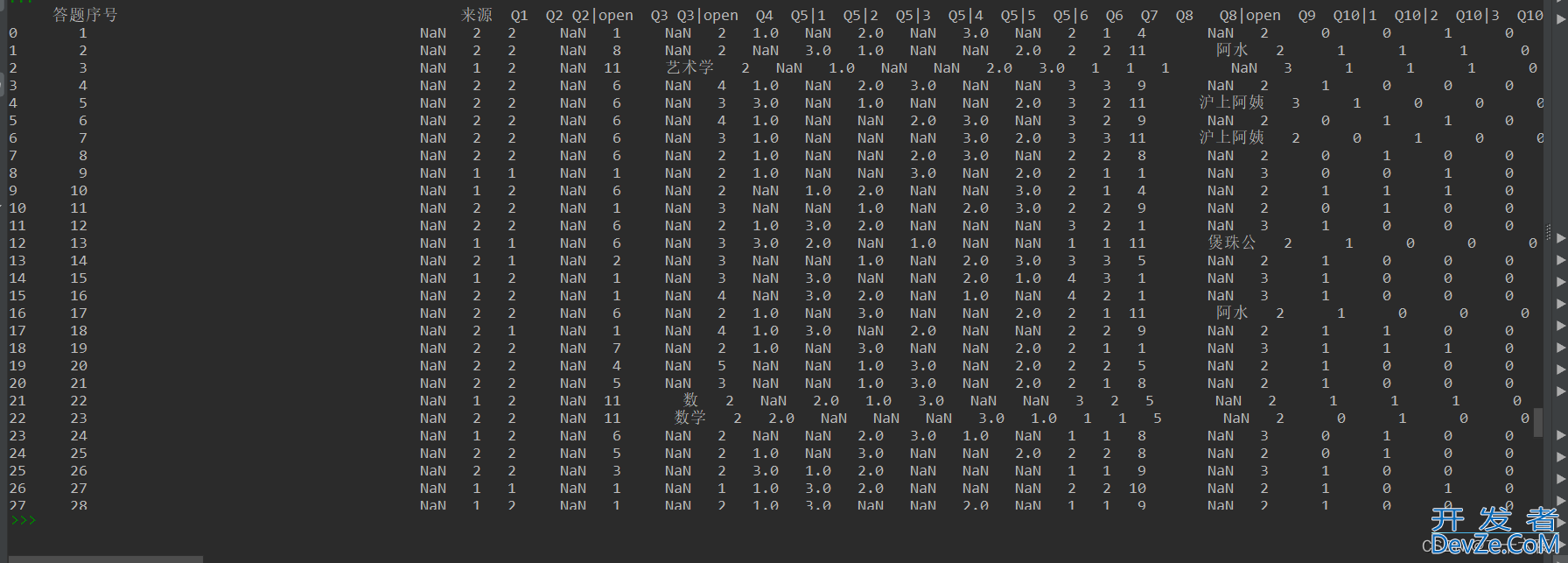
 导入excel表格具体可看我第一篇内容：如何在Python中导入EXCEL数据

 2.2 描述性统计分析所要计算的数据

通常，描述性统计分析需要各变量的观测值数量、均值、方差、标准差、最大最小值等，而在python中可运用库的方法计算出各个数据。详细代码见以下：

obs=df.count()#观测值
means=df.mean()#均值
var=df.var()#方差
std=df.std()#标准差
min=df.min()#最小值
max=df.max()#最大值
mode=df.mode()#众数
siyi=df.quantile(0.25)#四分之一位数
sisan=df.quantile(0.75)#四分之三位数
median=df.median()#中位数
skew=df.skew()#偏度
kurt=df.kurt()#峰度
print("最大值:\n",max,'\n',"最小值:\n",min,'\n','观测量:\n',obs,'\n','均值:\n',means,'\n',
      "方差:\n",var,"\n",'标准差:\n',std,'\n',"众数: ",mode,"\n",'四分之一位数:\n',siyi,'\n',
      '四分之三位数:\n',sisan,'\n','中位数:\n',median,'\n','偏度:\n',skew,'\n','峰度：\n',kurt)

代码的含义在注释中已经标注出来了，不再赘述。（print里的“\n”表示换行输出）在运行以上代码后，可以得到excel表格中每一列的对应数据，展示如下：

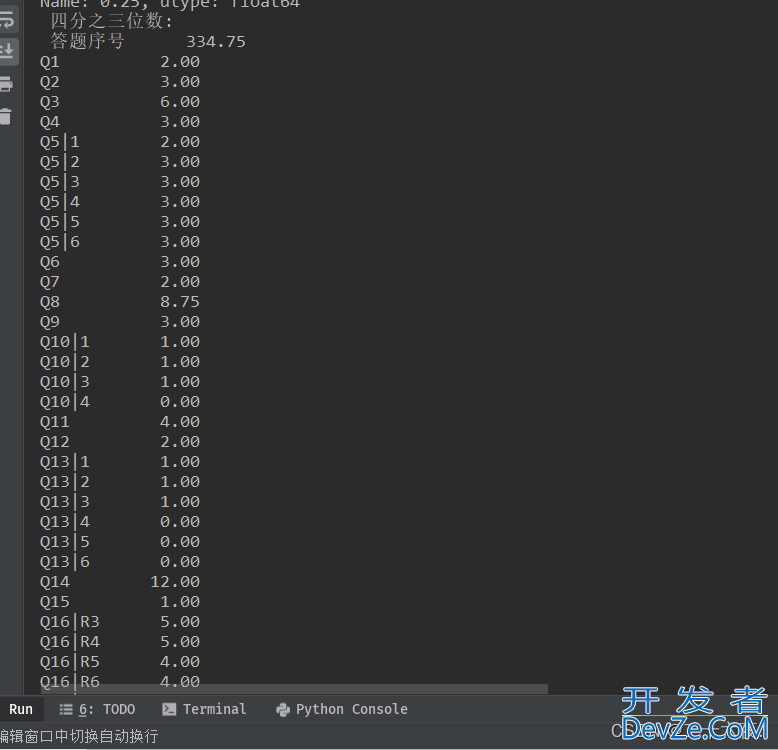
 输出的样式如上图，由于结果太多太长，就不一一展示。

2.3 数据可视化

2.3.1 概述

描述性统计分析中，除了列出以上的分析数据以外，在多数情况下仍然需要对重要的数据给出可视化的内容，即作图。数据可视化的图的类型有很多种，比如说折线图、柱状图、条形图、散点图、气泡图、雷达图、箱线图等。而在一般的数据分析类报告中，最常用的便是折线图、柱状图，因此在本篇中只介绍这两种可视化方法，其他的在后续教程分享中会按需要给出。

2.3.2 思路

可视化之前要有一个编写代码的思路，而作图的基本思路如下：

建立画布建立坐标系输入x轴数据与y轴数据设定x轴与y轴的刻度并给刻度命名作图2.3.3 编写代码 

fig=plt.figure()#建立画布
ax1=fig.add_subplot(1,1,1)#建立坐标系
 
x=np.arange(7)#x轴数据
y=np.array([jishu1,jishu2,jishu3,jishu4,jishu5,jishu6,jishu7])#y轴数据
 
plt.xticks(np.arange(7),['0-50元','50-100元','100-150元','150-200元','200-250元','250-300元','300元及以上'])#x轴长度与命名
plt.yticks(np.arange(0,350,50))#y轴长度与命名
plt.plot(x,y)#作图

建立坐标系：

建立坐标系中，add_subplot()方法括号里的数字的含义是：一行一列的第一个坐标系。这么说可能有点抽象，我给出以下例子：

#代码1：
fig=plt.figure()#建立画布
ax1=fig.add_subplot(1,1,1)#建立坐标系
 
#代码2：
fig=plt.figure()#建立画布
ax1=fig.add_subplot(2,2,1)#建立坐标系1
ax2=fig.add_subplot(2,2,2)#建立坐标系2
ax3=fig.add_subplot(2,2,3)#建立坐标系3
ax4=fig.add_subplot(2,2,4)#建立坐标系4

代码1中的（1，1，1）表示一行一列的第一个坐标系；代码二中的（2，2，1）表示二行二列的第一个坐标系，（2，2，2）表示二行二列的第二个坐标系，（2，2，3）表示二行二列的第三个坐标系，（2，2，4）表示二行二列的第四个坐标系。

而这两段代码展示出的坐标图是不一样的，见下图：

代码1：

 代码2：

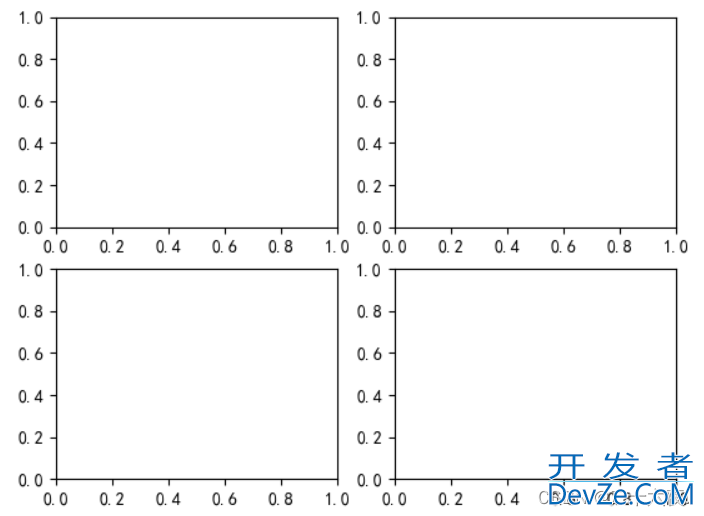
 对比两个输出结果，可以很容易地知道，代码1一张图中只作了一个坐标系，而代码2的一张图中作出了四个坐标系。一行一列的第一个坐标系指的就是代码1唯一的这一个坐标系，而二行二列的第一个坐标系指的是左上角的坐标系，二行二列的第四个坐标系指的是右下角的坐标系。这样应该就能比较好地理解这个函数的意义了。

附上数据（坐标）：

看到x与y轴数据的代码，其中np.arange()函数是调用的np库的函数方法。arange()中，方法与range()长的比较像：arange(start,end,step)。具体含义可以查看后续基础篇分享。若了解range()函数的话，那么arange(7)中的数字7的含义我也不用多说。x=np.arange(7)则表示横坐标x分别等于0，1，2，3，4，5，6时对应的情况。对于y中的array()函数，其主要是用于矩阵或数组的输入的，而本篇中的代码：y=np.array([jishu1,jishu2,jishu3,jishu4,jishu5,jishu6,jishu7])，其中的jishu1这一系列的命名是我定义的变量名，其具体含义我在后文补充，总之在array()中需要输入的也是数字。（按照各个问题的需要，本篇使用了array()，而x与y都适用np.arange()来输入数据都是可以的）。

由此，x与y的开发者_C教程数值组成了一个坐标（x，y），从而能定义一个点的位置。

设定刻度（又可称长度）与名称：

最后三行代码中的plt.xticks()与plt.yticks()方法分别是为了设定坐标刻度（又可称长度）与名称准备的。其中，括号内的方法为：（刻度，命名），而np.arange(7)表示横坐标轴设定的长度为7，列表['0-50元','50-100元','100-150元','150-200元','200-250元','250-300元','300元及以上']即每一个刻度的命名。

最后一行代码则是作出符合以上条件的坐标图。

其结果展示如下：

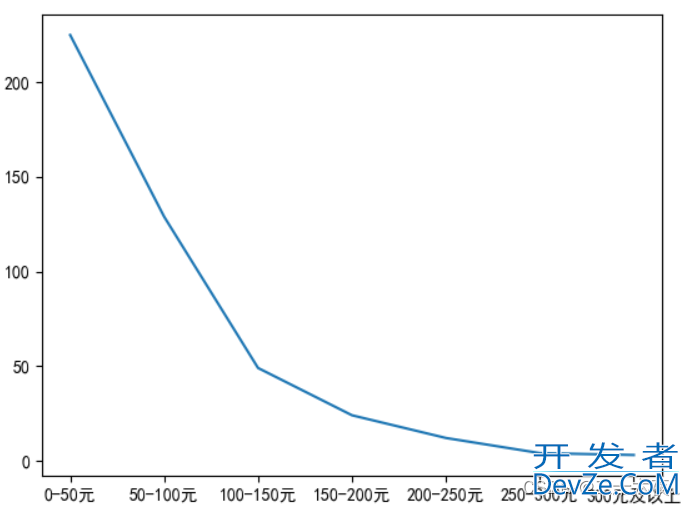
 显而易见，x轴的刻度编程了我所设定的名称，y轴没有设定名称，则以数值的形式出现。

为了使坐标图更加直观，我们也可以给x轴和y轴赋上标签，代码如下：

plt.xlabel('消费金额')#x轴的标签
plt.ylabel('人数')#y轴的标签

此时坐标图如下：

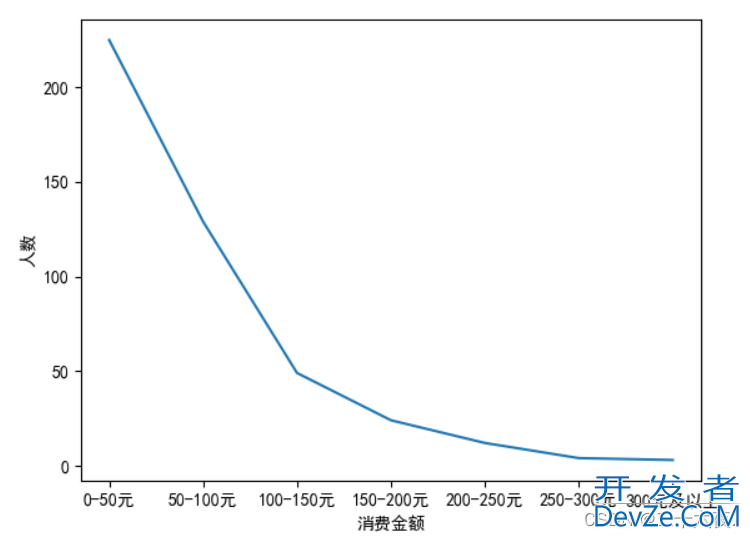
 对比前面的坐标图，此时的坐标图中x轴和y轴都有了它们的“名字”，这样图的关系就更加明朗了。

2.4 补充内容

前面提到，array()函数中的列表是什么意思。我是以我自己所收集的数据为例，写的本篇内容，因此有的地方是看个人研究需要而写的代码，在该部分我加以解释。

Q7=df.iloc[:,15]
q7=[]
for i in Q7:
      q7.append(i)
print(q7)#读取所要分析的列的数据
jishu1=int(q7.count(1))
jishu2=int(q7.count(2))
jishu3=int(q7.count(3))
jishu4=int(q7.count(4))
jishu5=int(q7.count(5))
jishu6=int(q7.count(6))
jishu7=int(q7.count(7))#计数
print('0-50元的有：',jishu1,'\n','50-100元的有：',jishu2,'\n','100-150元的有：',jishu3,'\n',
      '150-200元的有：',jishu4,'\n','200-250元的有：',jishu5,'\n','250-300元的有：',jishu6,'\n','300元及以上的有：',jishu7,'\n')

第一行的df.iloc[:,15]表示的含义是我要读取第十五列的变量的数据，该内容为“选取excel表格中的某一列”的方法的内容，属于基础篇的操作，在后续我会在基础篇中分享给部分的内容，不在此地赘述。

下面的循环是我将读取的函数放入列表中，并用count()函数计算个数（该数据为人数计数，因此count()实际上是在数人数），由此得出以下各个消费段的人数，输出结果如下：

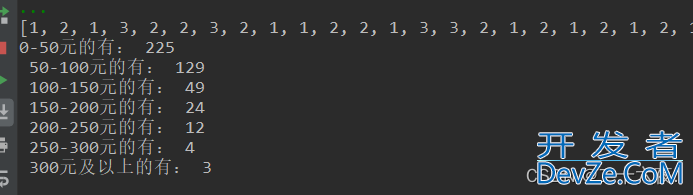
 这七个数值就是y轴输入的数据。由此应该就能理解我在编写y轴输入数据的代码时列表里的几个变量名是啥意思了。

三、完整代码与总结

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
pd.set_option('display.max_columns',1000)
pd.set_option("display.width",1000)
pd.set_option('display.max_colwidth',1000)
pd.set_option('display.max_rows',1000)#将行和列的最大展示值设置到1000，则可展示更多的行而不是以省略号形式展示。
df=pd.read_excel(r'D:\杂货\编码数据.xlsx',sheet_name='编码数据')
obs=df.count()#观测值
means=df.mean()#均值
var=df.var()#方差
std=df.std()#标准差
min=df.min()#最小值
max=df.max()#最大值
mode=df.mode()#众数
siyi=df.quantile(0.25)#四分之一位数
sisan=df.quantile(0.75)#四分之三位数
median=df.median()#中位数
skew=df.skew()#偏度
kurt=df.kurt()#峰度
print("最大值:\n",max,'\n',"最小值:\n",min,'\n','观测量:\n',obs,'\n','均值:\n',means,'\n',
      "方差:\n",var,"\n",'标准差:\n',std,'\n',"众数: ",mode,"\n",'四分TmeXArmkA之一位数:\n',siyi,'\n',
      '四分之三位数:\n',sisan,'\n','中位数:\n',median,'\n','偏度:\n',skew,'js\n','峰度：\n',kurt)
 
#作图
Q7=df.iloc[:,15]
q7=[]
for i in Q7:
      q7.append(i)
print(q7)#读取所要分析的列的数据
jishu1=int(q7.count(1))
jishu2=int(q7.count(2))
jishu3=int(q7.count(3))
编程jishjsu4=int(q7.count(4))
jishu5=int(q7.count(5))
jishu6=int(q7.count(6))
jishu7=int(q7.count(7))#计数
print('0-50元的有：',jishu1,'\n','50-100元的有：',jishu2,'\n','100-150元的有：',jishu3,'\n',
      '150-200元的有：',jishu4,'\n','200-250元的有：',jishu5,'\n','250-300元的有：',jishu6,'\n','300元及以上的有：',jishu7,'\n')
 
fig=plt.figure()#建立画布
ax1=fig.add_subplot(1,1,1)#建立坐标系
 
x=np.arange(7)#x轴数据
y=np.array([jishu1,jishu2,jishu3,jishu4,jishu5,jishu6,jishu7])#y轴数据
 
plt.xticks(np.arange(7),['0-50元','50-100元','100-150元','150-200元','200-250元','250-300元','300元及以上'])#x轴长度与命名
plt.yticks(np.arange(0,350,50))#y轴长度与命名
plt.plot(x,y)#作图
plt.xlabel('消费金额')#x轴代表的名字
plt.ylabel('人数')#y轴代表的名字

到此这篇关于如何使用Python程序完成描述性统计分析需求的文章就介绍到这了,更多相关Python完成描述性统计分析内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！