Differences between FFTW and CUFFT output
In the char I have posted below, I am comparing the results from an IFFT run in FFTW and CUFFT.
What are the possible reasons this is coming out different? Is it really THAT much round off error?
Here is the relevant code snippet:
cufftHandle plan;
cufftComplex *d_data;
cufftComplex *h_data;
cudaMalloc((void**)&d_data, sizeof(cufftComplex)*W);
complex<float> *temp = (complex<float>*)fftwf_malloc(sizeof(fftwf_complex) * W);
h_data = (cufftComplex *)malloc(sizeof(cufftComplex)*W);
memset(h_data, 0, W*sizeof(cufftComplex));
/* Create a 1D FFT plan. */
cufftPlan1d(&plan, W, CUFFT_C2C, 1);
if (!reader开发者_如何学运维->getData(rowBuff, row))
return 0;
// copy from read buffer to our FFT input buffer
memcpy(indata, rowBuff, fCols * sizeof(complex<float>));
for(int c = 0; c < W; c++)
h_data[c] = make_cuComplex(indata[c].real(), indata[c].imag());
cutilSafeCall(cudaMemcpy(d_data, h_data, W* sizeof(cufftComplex), cudaMemcpyHostToDevice));
cufftExecC2C(plan, d_data, d_data, CUFFT_INVERSE);
cutilSafeCall(cudaMemcpy(h_data, d_data,W * sizeof(cufftComplex), cudaMemcpyDeviceToHost));
for(int c = 0; c < W; c++)
temp[c] =(cuCrealf(h_data[c]), cuCimagf(h_data[c]));
//execute ifft plan on "indata"
fftwf_execute(ifft);
...
//dump out abs() values of the first 50 temp and outdata values. Had to convert h_data back to a normal complex
ifft was defined like so:
ifft = fftwf_plan_dft_1d(freqCols, reinterpret_cast<fftwf_complex*>(indata),
reinterpret_cast<fftwf_complex*>(outdata),
FFTW_BACKWARD, FFTW_ESTIMATE);
and to generate the graph I dumped out h_data and outdata after the fftw_execute W is the width of the row of the image I am processing.
See anything glaringly obvious?
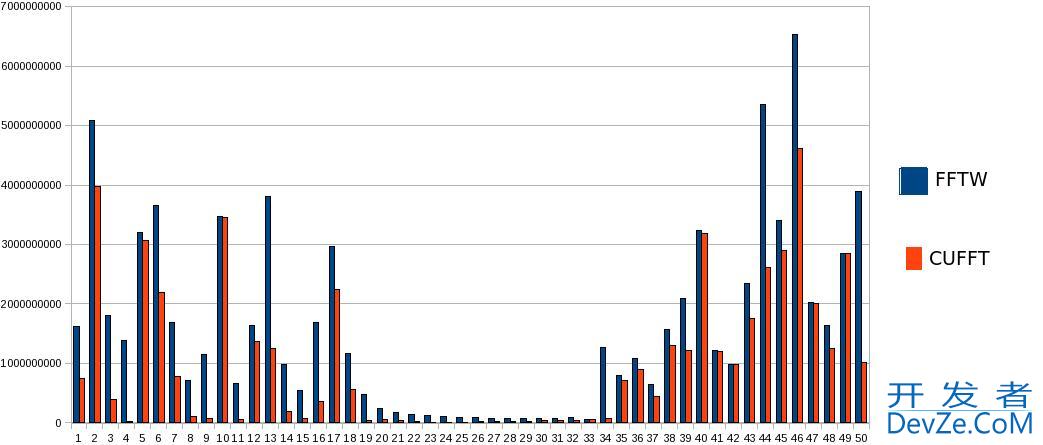
So it looks like CUFFT is returning a real and imaginary part, and FFTW only the real. The cuCabsf() function that comes iwth the CUFFT complex library causes this to give me a multiple of sqrt(2) when I have both parts of the complex
As an aside - I never have been able to get exactly matching results in the intermediate steps between FFTW and CUFFT. If you do both the IFFT and FFT though, you should get something close.
 加载中,请稍侯......
加载中,请稍侯......
精彩评论