拓扑排序Python实现的过程

目录

• 有向无环图
• 拓扑排序
• 算法步骤
• 代码实现
• 总结

有向无环图

拓扑排序是针对有向无环图（DAG, Directed javascriptAcyclic Graph）的

具有以下性质：

• 如果这个图不是 DAG，那么它是没有拓扑序的；
• 如果是 DAG，那么它至少有一个拓扑序；
• 反之，如果它存在一个拓扑序，那么这个图必定是 DGA。

拓扑排序

对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序，是将G中所有顶点排成一个线性序列，使得图中任意一对顶点u和v，若边(u,v)∈E(G)，则u在线性序列中出现在v之前。

通常，这样的线性序列称为js满足拓扑次序(Topological Order)的序列，简称拓扑序列。

简单的说，由某个集合上的js一个偏序得到该集合上的一个全序，这个操作称之为拓扑排序。

算法步骤

在讲算法步骤之前先了解入度与出度的概念：

• 入度：顶点的入度是指「指向该顶点的边」的数量；
• 出度：顶点的出度是指该顶点指向其他点的边的数量。

可以理解为入度为0的点就是起点，拓扑排序步骤如下：

• 从 DAG 图中选择一个入度为0的顶点并输出；
• 从图中删除该顶点和所有以它为起点的有向边；
• 重复 1 和 2 直到当前的 DAG 图为空或当前图中不存在入度为0的顶点为止。后一种情况说明有向图中必然存在环

代码实现

对于下图：

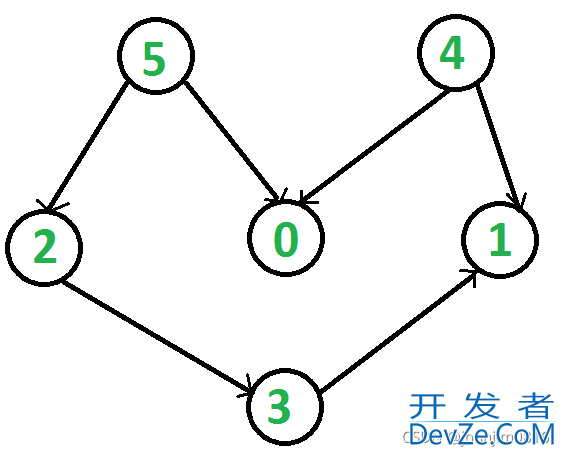
from collections import defaultdict 
 
class Graph: 
    def __init__(self,vertices): 
        self.graph = defaultdict(list) 
       cjosjHZl self.V = vertices
  
    def addEdge(self,u,v): 
        self.graph[u].append(v) python
  
    def topologicalSortUtil(self,v,visited,stack): 
  
        visited[v] = True
  
        for i in self.graph[v]: 
            if visited[i] == False: 
                self.topologicalSortUtil(i,visited,stack) 
  
        stack.insert(0,v) 
  
    def topologicalSort(self): 
        visited = [False]*self.V 开发者_C开发
        stack =[] 
  
        for i in range(self.V): 
            if visited[i] == False: 
                self.topologicalSortUtil(i,visited,stack) 
  
        print (stack) 
  
g= Graph(6) 
g.addEdge(5, 2); 
g.addEdge(5, 0); 
g.addEdge(4, 0); 
g.addEdge(4, 1); 
g.addEdge(2, 3); 
g.addEdge(3, 1); 
  
print ("拓扑排序结果：")
g.topologicalSort() # 结果为[5, 4, 2, 3, 1, 0]

总结

以上为个人经验，希望能给大家一个参考，也希望大家多多支持我们。