Python图像处理之图像清晰度评价

目录

• 0、实现效果
• 1、概述
• 2、模糊度分类
• 3、清晰度量化指标
• Brenner
• 能量梯度函数(Energy of Gradient)
• Roberts
• Laplace
• SMD（灰度方差）函数
• SMD2 （灰度方差乘积）函数
• 4、图像清晰度评价实现
• 5、总结与评价

0、实现效果

能够通过一张标准图，对同一组相机拍摄的照片进行清晰度评价。

1、概述

图像清晰度是用来指导调焦机构找到正焦位置的评价函数。理想的清晰度评价曲线类似于泊松分布，请看下图：

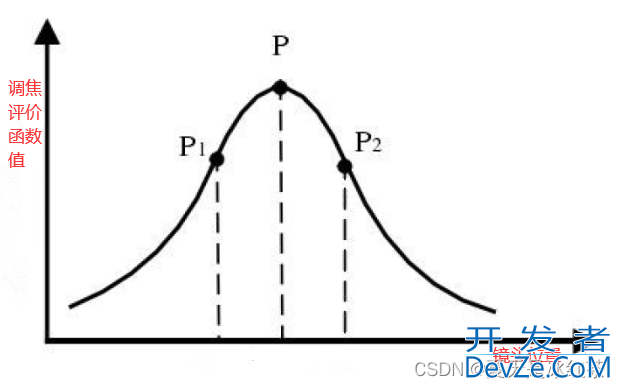
p点对应于正焦位置，P1 和P2编程客栈 为正焦位置焦前和焦后采集到图像的清晰度评价结果。

正焦的图像比模糊的离焦图像边缘要更加的锐利清晰，相应的边缘像素灰度值变化大，因而会有更大的梯度值，从数学的角度来看图像，它是二维的离散矩阵，利用梯度函数可获开发者_开发培训取图像的灰度信息，来判别图像的清晰度，在离散信中梯度表现为差分形式。

2、模糊度android分类

1、运动模糊

运动模糊是在捕获图像时，快门在打开时间内成像系统和拍摄 对象的短暂相对运动，造成成像在某个方向上形成的模糊。

2、压缩模糊

压缩模糊是图像在进行有损压缩丢失部分信息。

3、高斯模糊

高斯模糊是人为引入的一种模糊，使用高斯低通滤波器对原始图像进行滤波得到的。

3、清晰度量化指标

Brenner

Brenner梯度函数是最简单的梯度评价函数，它只是简单的计算相邻两个像素灰度差的平方，该函数定义如下：

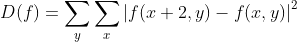
f(x,y) 表示图像f对应像素点(x,y)的灰度值，D(f)为图像清晰度计算结果。

python实现：

def brenner(img):
    '''
    :param img:narray 二维灰度图像
    :return: int 图像越清晰越大
    '''
    shapes = np.shape(img)
    output = 0
    for x in range(0, shapes[0]-2):
        for y in range(0, shapes[1]):
            output+=(int(img[x+2,y])-int(img[x,y]))**2
    return output

能量梯度函数(Energy of Gradient)

将 x 方向和 y 方向的相邻像素的灰度值之差的平方和作为每个像素点的梯度值，对所有像素梯度值累加作为清晰度评价函数值，表达式如下所示：

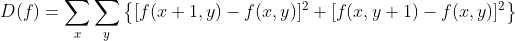
python实现：

def EOG(img):
    '''
 python   :param img:narray 二维灰度图像
    :return: int 图像越清晰越大
    '''
    shapes = np.shape(img)
    output = 0
    for x in range(0, shapes[0]-1):
        for y in range(0, shapes[1]-1):
            output+=((int(img[x+1,y])-int(img[x,y]))**2+(int(img[x,y+1])-int(img[x,y]))**2)
    return output

Roberts

Roberts函数与能量梯度函数相似，它是利用对角方向像素点灰度值之差。将4个相邻像素点的灰度值交叉相减的平方和作为每个像素点的梯度值，对所有像素梯度值累加作为清晰度评价函数值，表达式如下式所示：

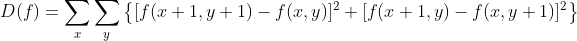
python实现：

def Roberts(img):
    '''
    :param img:narray 二维灰度图像
    :return: int 图像越清晰越大
    '''
    shapes = np.shape(img)
    output = 0
    for x in range(0, shapes[0]-1):
        for y in range(0, shapes[1]-1):
            output+=((int(img[x+1,y+1])-int(img[x,y]))**2+(int(img[x+1,y])-int(img[x,y+1]))**2)
    return output

Laplace

采用Laplace算子与图像各个像素点的灰度值进行卷积得到一个梯度矩阵记为，取各像素点梯度的平方和作为评价函数，如下式所示：

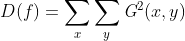
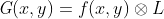
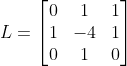
python实现：

def Laplacian(img):
    '''
    :param img:narray 二维灰度图像
    :return: int 图像越清晰越大
    '''
    return cv2.Laplacian(img,cv2.CV_64F).var()

由于之前推导过，你可以查看此文，这是我以前所写的一篇博客:图像处理：边缘检测原理

SMD（灰度方差）函数

当完全聚焦时，图像最清晰，图像中的高频分量也最多，故可将灰度android变化作为聚焦评价的依据，灰度方差法的公式如下：

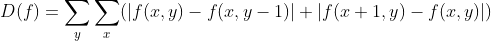
python实现：

def SMD(img):
    '''
    :param img:narray 二维灰度图像
    :return: int 图像越清晰越大
    '''
    shape = np.shape(img)
    output = 0
    for x in range(1, shape[0]-1):
        for y in range(0, shape[1]):
            output+=math.fabs(int(img[x,y])-int(img[x,y-1]))
            output+=math.fabs(int(img[x,y]-int(img[x+1,y])))
    return output

SMD2 （灰度方差乘积）函数

SDM函数具有较好的计算性能，但其缺点也很明显，即在焦点附近python灵敏度不高，即该函数在极值点附近过于平坦，从而导致聚焦精度难以提高。在《一种快速高灵敏度聚焦评价函数》中李郁峰等人在论文中提出了一种新的评价函数，称之为灰度方差乘积法，即对每一个像素领域两个灰度差相乘后再逐个像素累加，该函数定义如下：

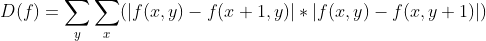
python实现：

def SMD2(img):
    '''
    :param img:narray 二维灰度图像
    :return: int 图像约清晰越大
    '''
    shape = np.shape(img)
    output = 0
    for x in range(0, shape[0]-1):
        for y in range(0, shape[1]-1):
            output+=math.fabs(int(img[x,y])-int(img[x+1,y]))*math.fabs(int(img[x,y]-int(img[x,y+1])))
    return output

4、图像清晰度评价实现

SWD2:

import cv2
import pyps.pyzjr.definition as din
import pyps.pyzjr.utility as ult
 
 
image=ult.read_resize_image("./compare/8881.jpg",space=True)
img = din.SMD2(image)
print(img)
 
cv2.putText(image, f"definition:{img:.2f}", (10, 30),
            cv2.FONT_HERSHEY_SIMPLEX, 0.8, (0, 0, 255), 3)
cv2.imshow("definition_Image", image)
 
cv2.waitKey(0)

Brenner:

Laplacian:

5、总结与评价

很遗憾，本次的清晰度评价失败了，如果想要得到一个边界值几乎不可能实现，哪怕通过大量图像数据（模糊图像与清晰图像）也不能完成，因为这些清晰度量化指标函数都是通过求图像像素的梯度，换汤不换药，在不同场景不同模糊的条件下很难去进行比对。

到此这篇关于Python图像处理之图像清晰度评价的文章就介绍到这了,更多相关Python图像清晰度评价内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！