C++前缀和及用法示例详解

目录

• 1.什么是前缀和
• 2.前缀和的过程
• 1.文字
• 2.图示
• 3.前缀和的用法
• 1.前缀和的定义
• 2.预处理前缀和数组
• 3.查询区间和
• 4.数组中某个区间的和是否为特定值
• 5.数组中连续子数组的和的最大值
• 6.数组中连续子数组的和的最小值
• 7.举例
• 4.用处
• 5.例题
• 6.总结

1.什么是前缀和

C++前缀和是一种常用的算法，用于解决求解区间和问题。前缀和数组是一个长度为n的数组，其中第i个元素代表原始数组从下标0到下标i的元素之和。通过预先计算前缀和数组，可以在O(1)的时间复杂度内求解任意区间的和。

前缀和算法的基本思想是利用动态规划的思想，通过累加计算出每一个位置的前缀和。具体实现时，可以对原始数组进行一次遍历，累加计算出前缀和数编程组的每一个元素。

2.前缀和的过程

1.文字

前缀和它的基本思想是通过提前计算数组的前缀和，可以在O(1)的时间复杂度内求解任意子数组的和。下面我用文字详细描述前缀和的过程，并用表格举例演示。

1. 首先，我们定义一个数组，假设数组为arr，长度为n。我们需要额外定义一个长度为n+1的数组prefix_sum，用于存储arr数组的前缀和。

2. 计算前缀和的过程如下：

   - 首先，初编程客栈始化prefix_sum[0]为0，表示arr的前0个元素的和为0。

   - 然后，从1开始遍历数组arr，逐个计算每个位置的前缀和，即prefix_sum[i] = prefix_sum[i-1] + arr[i-1]。

3. 最终，prefix_sum中存储了arr数组的前缀和，prefix_sum[i]表示arr前i个元素的和。

2.图示

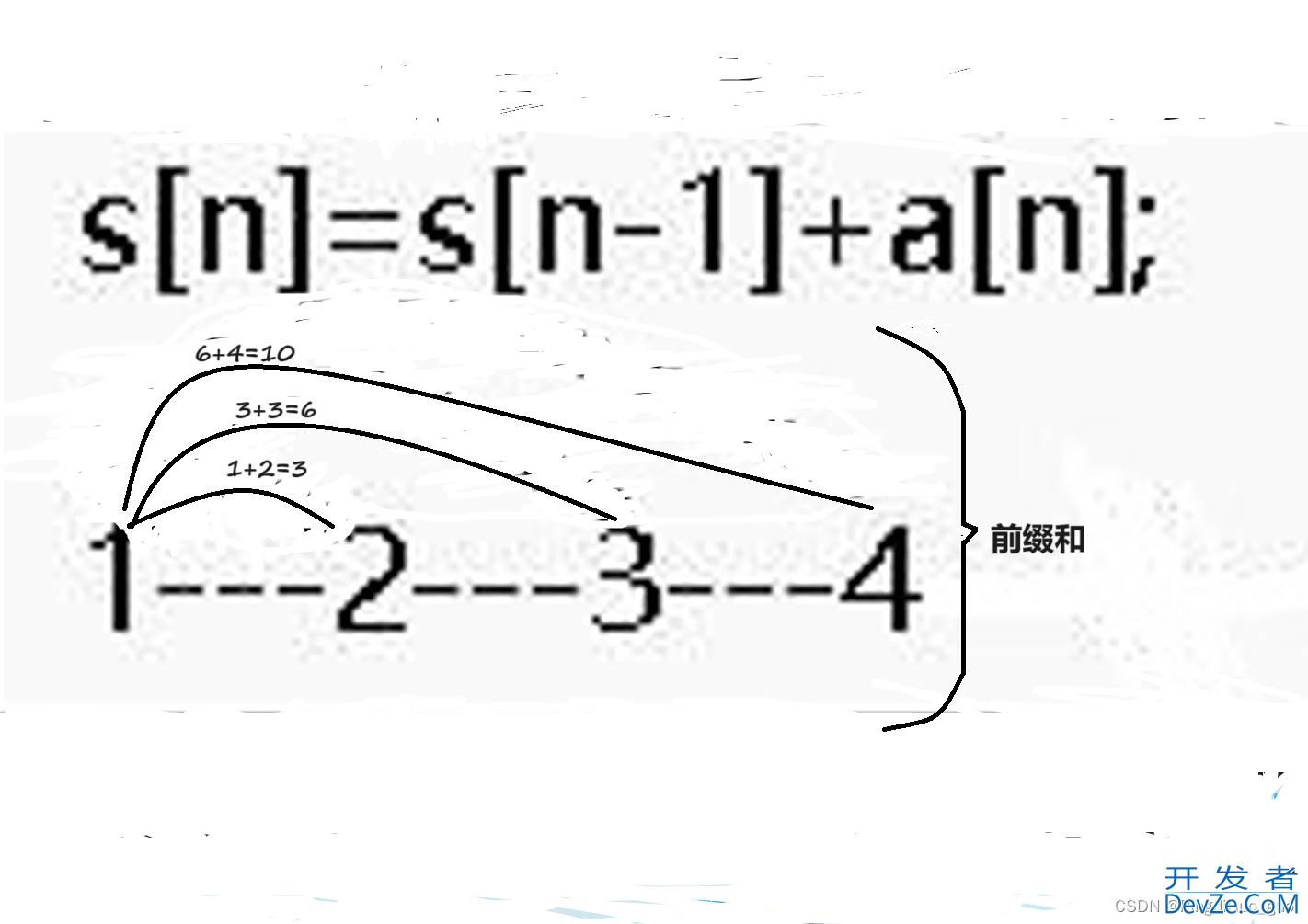
下面通过一个具体的例子来说明前缀和的计算过程：

假设arr = [1, 2, 3, 4, 5]，长度为5，我们要计算其前缀和。

| arr索引 | 元素值 | 前缀和计算过程           | prefix_sum值 |

|---------|--------|-------------------------|--------------|

| 0       | 1      | prefix_sum[0] = 0 + 1    | 1            |

| 1       | 2      | prefix_sum[1] = 1 + 2    | 3            |

| 2       | 3      | prefix_sum[2] = 3 + 3    | 6            |

| 3       | 4      | prefix_sum[3] = 6 + 4    | 10           |

| 4       | 5      | prefix_sum[4] = 10 + 5   | 15           |

通过这个表格，我们可以看到prefix_sum数组中存储了arr数组的前缀和。这样，在求解任意子数组的和时，只需要通过prefix_sum数组中的值进行简单的减法运算即可，实现了高效的求解过程。

3.前缀和的用法

C++前缀和是指在一个数组中，计算从数组起始位置到当前位置的所有元素的和。它的用途是在一些需要频繁查询某个区间和的场景中，可以通过预处理数组得到前缀和数组，从而在O(1)的时间复杂度内得到任意区间的和。

前缀和的用法可以分为以下几点：

1.前缀和的定义

在C++中，可以使用一个额外的数组来保存原始数组中每个位置的前缀和，即累加前面所有元素的和。下面是一个示例代码：

#include <IOStream>
#include <vector>
using namespace std;
vector<int> prefixSum(vector<int>& nums) {
    int n = nums.size();
    vector<int> prefix(n);
    prefix[0] = nums[0];  // 第一个元素的前缀和就是其本身
    // 计算前缀和
    for (int i = 1; i < n; i++) {
 python       prefix[i] = prefix[i-1] + nums[i];
    }
    return prefix;
}
int main() {
    vector<int> nums = {1, 2, 3, 4, 5};
    vector<int> prefix = prefixSum(nums);
    for (int num : prefix) {
        cout << num << " ";
    }
    cout << endl;
    return 0;
}

上述代码中，prefixSum函数接受一个整型数组作为参数，并返回一个新的数组，其中保存了每个位置的前缀和。

在prefixSum函数中，首先创建了一个与原始数组大小相同的prefix数组，用于保存前缀和。然后，对于数组中的每个元素，通过累加前面所有元素的和来计算当前位置的前缀和。最后，返回计算得到的前缀和数组。

在main函数中，我们将一个示例数组传入prefixSum函数，然后遍历输出计算得到的前缀和数组。

2.预处理前缀和数组

首先需要遍历原始数组，计算出每个位置的前缀和，并将其存储在一个新的数组中。具体的计算方法是，对于位置i，前缀和数组的第i个元素等于原始数组中前i个元素的和。

3.查询区间和

一旦得到了前缀和数组，就可以通过查询两个位置的前缀和来计算任意区间的和。对于一个区间[a, b]，其和等于前缀和数组中第b个元素减去第a-1个元素（如果a不等于1）。

4.数组中某个区间的和是否为特定值

通过前缀和计算区间和后，可以用哈希表记录出现的前缀和，以便在后续查询中快速判断。

5.数组中连续子数组的和的最大值

通过前缀和计算各个子数组的和，找出最大的子数组和。可以使用动态规划或遍历的方式实现。

6.数组中连续子数组的和的最小值

通过前缀和计算各个子数组的和，找出最小的子数组和。可以使用动态规划或遍历的方式实现。

7.举例

假设有一个数组arr = {1, 2, 3, 4, 5}，我们可以通过预处理得到前缀和数组prefixSum = {1, 3, 6, 10, 15}。然后，我们可以通过查询prefixSum - prefixSum[1-1]来计算区间[2, 4]的和，即6 - 1 = 5。

总结一下，C++前缀和的用法包括预处理前缀和数组和查询区间和。通过预处理数组，可以在O(1)的时间复杂度内得到任意区间的和，从而提高了查询效率。

4.用处

前缀和是一种常见的算法技巧，通常应用于数组相关的问题中。它的主要用途包括：

1. 快速计算数组区间和：通过预先计算数组的前缀和，可以在O(1)的时间复杂度内快速计算任意区间的和，而不需要每次都重新遍历计算。

2. 解决子数组和为特定值的问题：通过计算前缀和，在一维数组中可以快速找到和为特定值的子数组。

3. 解决数组中连续子数组的最大和问题：通过计算前缀和，可以优化求解连续子数组的最大和问题，使得时间复杂度可以达到O(n)。

4. 解决求解区间和的问题：通过利用前缀和的特性，可以在较快的时间内解决求解多个区间和的问题。

5. 判断两个子数组是否具有相同的和：通过计算不同位置的前缀和，可以快速判断两个子数组是否具有相同的和，用于一些比较问题中。

总的来说，前缀和在解决数组相关问题时具有非常重要的作用，可以优化计算效率，减少时间复杂度。

5.例题

题目描述：

给定一个包含 n 个非负整数的数组 nums，一个连续子数组的最大和被定义为该子数组中所有正数的和。设计一个算法，计算出数组中连续子数组的最大和。例如，对于数组 [-2, 1, -3, 4, -1, 2, 1, -5, 4]，连续子数组的最大和为 6，对应子数组 [4, -1, 2, 1]。

限制：

- 数组中的元素个数 n 满足 1 <= n <= 10^5

- 数组中的每个元素满足 -1000 <= nums[i] <= 1000

分析步骤：

1. 使用前缀和的方法，定义一个一维数组 prefixSum，其中 prefixSum[i] 表示前 i 个元素的和。

2. 对于任意子数组 [i, j] 的和可以表示为 prefixSum[j] - prefixSum[i-1]。

3. 遍历数组计算前缀和并更新最大子数组和，如果当前前缀和小于 0，则重新开始计算前缀和。

4. 最终，结果为更新过程中出现的最大子数组和。

代码实现（C++）：

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int maxSubarraySum(vector<int>& nums) {
    int n = nums.size();
    if (n == 0) return 0;
    vector<int> prefixSum(n);
    prefixSum[0] = nums[0];
    int maxSum = nums[0];
    for (int i = 1; i < n; i++) {
        prefixSum[i] = prefixSum[i-1] + nums[i];
        maxSum = max(maxSum, nums[i]);
        if (prefixSum[i] - prefixSum[i-1] > nums[i]) {
            prefixSum[i] = nums[i];
        }
        maxSum = max(maxSum, prefixSum[i]);
    }
    return maxSum;
}
int main() {
    vector<int> nums = {-2, 1, -3, 4, -1, 2, 1, -5, 4};
    cout << maxSuPmrowbUFMhbarraySum(nums) << endl;  // 输出 6
    return 0;
}

时间复杂度分析：

- 遍历数组一次，计算前缀和和更新最大子数组和，时间复杂度为 O(n)。

- 空间复杂度为 O(n)，用于存储前缀和数组。

这道题目利用前缀和的方法可以较为简洁地解决，但需要对连续子数组的性质有一定的理解和分析，算法的设计相对较难一些。

6.总结

本篇博客到这里就结束了，感谢大家的javascript支持与观看，如果大家有好的建议欢迎留言！

到此这篇关于C++前缀和的文章就介绍到这了,更多相关C++前缀和内容请搜索编程客栈(www.devze.com)以前的文章或继续浏览下面的相关文章希望大家以后多多支持编程客栈(www.devze.com)！