Python使用大语言模型进行图表可视化

目录

• 一、使用大模型生成代码进行可视化
• 画图一：使用python 绘制柱图
• 画图二、使用Python 绘制直方图
• 画图三、使用Python 绘制箱线图
• 画图四、使用Python 绘制二组数据的散点图
• 画图五、使用Python 绘制山脊图
• 使用Python 生成和预览数据
• 数据检验
• 二、动态图表
• 三、画图的美化
• 1、Matplotx
• 2、案例图形
• 3、其他工具

Python使用matplotlib进行可视化一直有2个问题，一是代码繁琐，二是默认模板比较丑。因此发展出seaborn等在matplotlib上二次开发，以更少的代码进行画图的和美化的库，但是这也带来了定制化不足的问题。在大模型时代，这个问题有了另一种解法，即使用大模型直接生成代码，解决了代码繁琐（代码虽长但不用手写）的问题。

一、使用大模型生成代码进行可视化

使用大模型生成想要的代码需要精准的提示词描述，否则大模型会根据自己的理解画图。为了让大模型能够精准的理解我们的意图，我把画图的设置进行了整理。同时把大模型生成的代码中的最佳实践列出来，便于大模型按照最佳的方法输出代码，避免大模型自创错误的方法。

需要画图时更改要求并把代码作为案例一并提交大模型生成代码。下面的需求是给大模型的输入所以，为了让大模型输出更精准，所以把关键把代码和自然语言混编。

本文主要解决三个问题

1、给出一个各类图标的基础设置提示词模板，保证大模型能一次性按需生成需要的模型，避免反复与大模型多轮对话。

2、给出代码的最佳实践和指定易错的API，避免大模型生成错误代码

3、各类图表的使用场景和样式。

画图一：使用Python 绘制柱图

使用Python画柱图，数据如下，其中x轴是 y轴是

1、使用颜色 #1E9ED9表示平均RSRP。

2、设置字体为汉字宋体。图标题字体为24，其他为18

3、全局设置mpl.rcParams[‘figure.dpi’] = 1080

4、每个 bar 显示标签，位置在bar的顶端而不是内部,label_type=‘edge’

5、bar无边框

6、纵轴标签为“平均RSRP（dbm）”从0开始

7、为了保障距离上边框的距离，纵轴最大刻度是ax.margins(y=0.2) ，顶部留20%空间

8、横轴标签为方案一、方案二。

9、横轴缩短每个bar的宽度和缩短两个bar 编程客栈间的距离。

10、横轴使用margin()函数让最右边的bar距离右边框和最左边的bar 距离左边框距离一致ax.margins(x=margin ) # 顶部留20%空间

核心布局参数系统

bar_width = 0.28 # 柱体宽度
bar_spacing = 0.12 # 柱间间距
margin = 0.12 # 新增边界控制参数 (建议范围0-0.3)

11、图标题为主覆盖站点选择

12、整个图像要加粗线的外边框

import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np

# 全局参数配置
mpl.rcParams['figure.dpi'] = 1080  # 设置分辨率
plt.rcParams['font.sans-serif'] = ['SimSun']  # 设置宋体
plt.rcParams['axes.unicode_minus'] = False   # 显示负号

# 核心数据与参数
data = [-89.68, -84.27]
labels = ['方案一', '方案二']
bar_color = '#1E9ED9'

# 布局控制系统
bar_width = 0.12      # 柱体宽度
bar_spacing = 0.28    # 柱间间距
margin = 0.24         # 边界对称控制参数

# 创建画布与坐标系
fig, ax = plt.subplots(figsize=(10, 7))

# 横坐标定位引擎
x_base = np.arange(len(labels))  # 基准定位点 [0, 1]
x_pos = x_base * (bar_width + bar_spacing)  # 精确柱体定位

# 绘制柱状图系统
bars = ax.bar(x_pos, data,
             width=bar_width,
             color=bar_color,
             edgecolor='none')  # 无边框设置

# 数据标签渲染器
ax.bar_label(bars,
            labels=[f'{v:.2f}' for v in data],
            label_type='edge',  # 将标签放置在柱子顶端
            padding=5,          # 调整标签与柱子顶端的距离
            fontsize=18,
            color='black')

# 坐标轴配置系统
ax.set_xticks(x_pos)
ax.set_xticklabels(labels, fontsize=18)
ax.set_ylabel('平均RSRP(dBm)', fontsize=18)
#ax.set_title('主覆盖站点选择', fontsize=24)

# 纵轴显示优化
ax.set_ylim(0, max(data) * 1.2)  # 强制从0开始
ax.invert_yaxis()  # 数值倒置显示
ax.margins(y=0.2)  # 顶部留20%空间

# 边界对称控制系统
ax.margins(x=margin)  # 左右对称留白

# 边框强化模块
for spine in ax.spines.values():
    spine.set_linewidth(2.5)  # 边框加粗

# 生成最终图像
plt.show()

画图二、使用Python 绘制直方图

使用Python 绘制频数分布直方图：

1、图像布局

• 使用颜色 #1E9ED9表示平均RSRP。
• 设置字体为汉字宋体，并解决负号显示问。
• 图标题字体为24，其他为18
• 图标题为：RSRP
• 全局设置mpl.rcParams[‘figure.dpi’] = 1080
• 图例放在右下角legend，去除外框。
• 在图像的右上角要加入plt.text 均值： 标准差：
• 为了保障距离上边框的距离，顶部留20%空间是ax.margins(y=0.2) ，

2、坐标轴

• x轴标签为方案一、方案二。
• y轴为“平均RSRP（dbm）” 从0开始，0在最下面。

3、标签和网格线

• 将标签放在柱子顶端，只显示非0标签。
• 相邻等高的柱子，标签要错开（可以去掉，bar等高标签防止重叠 from adjustText import adjust_text）
• 不显示网格线

4、其他元素

在均值的位置加一根红虚线

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.ticker import MaxNLocator
# 设置字体为宋体并解决负号显示问题
plt.rcParams['font.sans-serif'] = ['SimSun']  # 设置全局字体为宋体
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题

# 数据列表
data = [
    -92.3, -92.6, -86.6, -84.9, -89.2, -86, -87.9, -90.9, -87.9, -84.4,
    -89.1, -84.3, -96.9, -86.5, -88.7, -89.9, -88.7, -95, -89.7, -87.9,
    -84.6, -90.6, -91.4, -90.5, -86.3, -88, -90.6, -87.5, -88.7, -86.1
]

mean_value = sum(data) / len(data)
std_value = np.std(data)

plt.figure(figsize=(10, 6))
bins = np.linspace(-100, -80, 15)
n, bins, patches = plt.hist(data,
                            bins=bins,
  编程                          color='#1E9ED9',  # 使用颜色 #1E9ED9
                            edgecolor='black',
                            alpha=0.8)

# 在每个 bar 的顶端显示标签
for i, patch in enumerate(patches):
    height = n[i]
    if height > 0:  # 只显示非零高度的标签
        plt.text(patch.get_x() + patch.get_width() / 2, height + 0.1, str(int(height)),
                 ha='center', va='bottom', fontsize=10, fontname='SimSun')

# 添加均值红虚线，并设置图例标签
plt.axvline(x=mean_value, color='red', linestyle='--', label=f'均值: {mean_value:.2f} dBm')


# 设置标题和坐标轴标签
plt.title('RSRP数据分布直方图', fontsize=20)
plt.xlabel('RSRP值 (dBm)', fontsize=16)
plt.ylabel('频数', fontsize=16)

# 设置纵轴最大刻度并留出顶部空间
ax = plt.gca()
ax.margins(y=0.2)  # 纵轴顶部留 20% 空间
ax.yaxis.set_major_locator(MaxNLocator(integer=True))  # 纵轴刻度设置为整数

# 设置横轴范围
plt.xlim(-100, -80)  # 横轴从 -100 到 -80

# 添加图例
plt.legend(loc='lower right', fontsize=10, frameon=True, edgecolor='black')  # 图例在右上角

# 在图像右上角加入均值和标准差
plt.text(0.95, 0.95, f'均值: {mean_value:.2f} dBm\n标准差: {std_value:.2f} dBm',
         transform=ax.transAxes, fontsize=10, fontname='SimSun',
         verticalalignment='top', horizontalalignment='right',
         bbox=dict(boxstyle="round", facecolor="white", edgecolor="black"))

# 加粗所有边框
for spine in ax.spines.values():
    spine.set_linewidth(1.5)

# 调整布局
plt.tight_layout()

# 显示图像
plt.show()

画图三、使用Python 绘制箱线图

1、使用颜色 #DB472A作图。

2、设置字体为汉字宋体。

3、箱线图纵向显示

4、异常值用红点显示不要红点无边框

5、箱线图箱体填充

6、清空Y轴刻度系统ax.set_yticks([])

7、箱线图横放

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

# 全局参数设置
plt.rcParams['font.sans-serif'] = ['Arial']  # 替换为 Arial 字体
plt.rcParams['axes.unicode_minus'] = False

# 数据集
data = [
    13.15, 14.35, 14.15, 10.72, 16.35, 16.24, 15.42, 14.65, 10.87, 14.05,
    14.3, 12.83, 14.88, 16.69, 21.44, 15.96, 16.22, 15.16, 9.26, 15.32,
    15.59, 23.28, 14.78, 16.36, 15.29, 11.66, 19.06, 17.81, 17.93, 12.49
]

# 创建画布
fig, ax = plt.subplots()

# 绘制横向箱线图
box = ax.boxplot(data,
                 vert=编程客栈False,
                 patch_artist=True,
                 flierprops={'marker': 'o', 'markerfacecolor': 'red',
                             'markeredgecolor': 'none'},
                 boxprops={'color': '#DB472A', 'facecolor': '#DB472A'},
                 whiskerprops={'color': '#DB472A'},
                 capprops={'color': '#DB472A'},
                 medianprops={'color': 'white'})

# 计算统计量
mean_val = np.mean(data)
stats = [np.min(data), np.percentile(data, 25), np.median(
    data), np.percentile(data, 75), np.max(data)]

# 添加统计标注
ax.text(0.95, 0.95,
        f'中位数：{stats[2]:.2f}\n平均值：{mean_val:.2f}',
        transform=ax.transAxes,
        ha='right', va='top',
        fontsize=12,
        color='black',
        fontweight='bold',
        linespacing=1.5,
        bbox=dict(facecolor='white', alpha=0.7, edgecolor='none'))  # 添加背景框
ax.set_yticks([])  # 清空Y轴刻度系统

# 创建增强DataFrame
df = pd.DataFrame({
    "变量名称": ["数据集 A"],
    "最小值": [stats[0]],
    "Q1": [stats[1]],
    "中位数": [stats[2]],
    "Q3": [stats[3]],
    "最大值": [stats[4]],
    "平均值": [mean_val]
})

# 显示图表及数据
plt.title('箱线图')
plt.xlabel('数值分布')
plt.tight_layout()
plt.subplots_adjust(right=0.85)  # 增加右侧边距
plt.show()

# 打印 DataFrame
print(df)

画图四、使用Python 绘制二组数据的散点图

1、图像布局

• 使用颜色 #1E9ED9表示方案一、使用#DB472A表示方案二。方案一标记为圆形方案二为正方形。数据1为的标签为方案一和方案二。
• 设置字体为汉字宋体，并解决负号显示问。
• 图标题字体为24，其他为18
• 图标题为方案一和方案二对比散布图
• 全局设置mpl.rcParams[‘figure.dpi’] = 1080
• 图例放在右下角legend，去除外框。
• 在图像的右上角要加入plt.text 方案一均值 方案二 均值
• 为了保障距离上边框的距离，顶部留20%空间是ax.margins(y=0.2) ，

2、坐标轴

• x轴标签为1到30
• y轴为“平均RSRP（dbm）” 从-60 到-100

3、标签和网格线

• 不现实标签。2标签为方案一 均值：xx 使用f字符串实现，均值根据data计算
• 不显示网格线

4、其他元素

• 在给每组数据均值的位置加一根红虚线 案一的均值改为蓝色的虚线，两条虚线的上方都写上均值：xx 字体颜色与标记颜色相同
• 方案一标记为圆形方案二为正方形

import matplotlib.pyplot as plt
import numpy as np

# 全局参数设置
plt.rcParams['font.sans-serif'] = 'SimSun'
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['figure.dpi'] = 1080

# 准备数据
data1 = [-92.3,-92.6,-86.6,-84.9,-89.2,-86,-87.9,-90.9,-87.9,-84.4,
         -89.1,-84.3,-96.9,-86.5,-88.7,-89.9,-88.7,-95,-89.7,-87.9,
         -84.6,-90.6,-91.4,-90.5,-86.3,-88,-90.6,-87.5,-88.7,-86.1]
data2 = [
    -86.8, -86.7, -86.4, -84.7, -82.1, -85.1, -82.6, -81.7, -86.2, -81.8,
    -83.4, -85.8, -86.8, -84.2, -84.2, -90.3, -85.8, -83, -84.2, -88, -87.1,
    -83, -85.2, -86, -83.1, -85, -86.3, -86.3, -85.7, -84.1
]
x = np.arange(1, 31)

# 创建画布
fig, ax = plt.subplots(figsize=(10, 6))

# 计算均值
mean1 = round(np.mean(data1), 1)
mean2 = round(np.mean(data2), 1)

# 绘制散点图
ax.scatter(x, data1, c='#1E9ED9', marker='o', label='方案一')
ax.scatter(x, data2, c='#DB472A', marker='s', label='方案二')

# 添加均值虚线及标注
ax.axhline(mean1, color='blue', linestyle='--', linewidth=1)
ax.axhline(mean2, color='red', linestyle='--', linewidth=1)
ax.text(15.5, mean1-3, f'均值：{mean1}', color='blue', ha='right', fontsize=12)
ax.text(15.5, mean2+3, f'均值：{mean2}', color='red', ha='right', fontsize=12)

# 坐标轴设置
ax.set_xticks(x)
ax.set_ylim(-110, -70)
ax.set_ylabel('平均RSRP（dBm）', fontsize=18)
ax.yaxis.set_label_coords(-0.05, 0.5)

# 图例设置
ax.legend(loc='lower right', frameon=False, fontsize=18)

# 其他格式
ax.margins(y=0.2)
plt.title('RSRP散布图', fontsize=24)
ax.grid(False)
plt.tight_layout()
plt.show()

画图五、使用Python 绘制山脊图

使用joypy库绘山脊图

import pandas as pd
import matplotlib.pyplot as plt
from joypy import joyplot

# 用户提供的四组数据（修正命名）
data1 = [13.9, 16.7, 18.5, 15.1, 12.1, 13.3, 12.4, 15.5, 15.9, 15, 14, 15.3, 14.6, 14.4, 16, 18.2, 16.8, 15.9, 14.4, 15.1, 16.2, 14.1, 14.2, 16, 13.1, 12.9, 15.8, 18.4, 16.5, 16.4]
data2 = [17.1, 14.4, 15.6, 16.4, 14.3, 15.5, 19.3, 17.4, 16.2, 15.3, 17.8, 11.4, 13.8, 17.5, 16.5, 16.1, 16.8, 11.7, 17.8, 18.2, 17.1, 14.1, 17.3, 17.8, 16, 14.7, 16.1, 16.2, 15.3, 13.8]
data3 = [16.5, 13.3, 15.5, 14.3, 13.4, 20.3, 16, 16, 12.5, 17.7, 15.5, 16, 15.3, 16.1, 17.1, 16.8, 20.8, 17.5, 17, 14, 16.5, 15.9, 15.9, 18.4, 14.4, 14.3, 17.4, 16.5, 15.4, 18.1]
data4 = [17, 19.7, 16.5, 18, 18.5, 17.2, 20, 18.4, 16.7, 18.2, 18.2, 16.1, 16.3, 19.6, 17, 17.4, 21.2, 18.3, 18.2, 16.5, 17.9, 13.2, 14.4, 13.9, 18.9, 16.6, 17.7, 18.7, 15.9, 16]

# 转换为长格式DataFrame
df = pd.DataFrame({
    "方案1": data1,
    "方案2": data2,
    "方案3": data3,
    "方案4": data4
}).melt(var_name="Category", value_name="Value")

# 绘制山脊图
fig, axes = joyplot(
    data=df,
    by="Category",
    column="Value",
    figsize=(8, 6),
    overlap=0.8,       # 控制层叠高度
    colormap=plt.cm.viridis,  # 颜色映射
    title="Python使用大语言模型进行图表可视化",
    linecolor="white"  # 曲线颜色
)

plt.show()

使用Python 生成和预览数据

生成数据 、查看数据直方图 、查看箱线图、生成数据和其统计写入excel

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.ticker import MaxNLocator

# 生成数据集
np.random.seed(2023)

# 模拟生成 final_data 数据（假设其为一个长度为30的数组）
final_data = np.random.normal(loc=-89.1, scale=2, size=30)  # 示例数据

# 创建数据框架
df = pd.DataFrame({
    '测试批次': [f'第{i}次测试' for i in range(1, 31)],
    '平均RSRP': np.round(final_data, 1)
})

# 打印统计指标
mean_value = df['平均RSRP'].mean()
std_value = df['平均RSRP'].std(ddof=1)
print(f"平均值: {mean_value:.2f} dBm")
print(f"标准差: {std_value:.2f} dBm")

# 绘制直方图
plt.figure(figsize=(10, 6))
bins = np.linspace(-100, -80, 15)  # 设置横轴从 -100 到 -80 分桶
n, bins, patches = plt.hist(df['平均RSRP'],
                            bins=bins,
                            color='#1E9ED9',  # 使用颜色 #1E9ED9
                            edgecolor='black',
                            alpha=0.8)

# 在每个 bar 的顶端显示标签
for i, patch in enumerate(patches):
    height = n[i]
    if height > 0:  # 只显示非零高度的标签
        plt.text(patch.get_x() + patch.get_width() / 2, height + 0.1, str(int(height)),
                 ha='center', va='bottom', fontsize=10, fontname='SimSun')

# 添加均值红虚线
plt.axvline(x=mean_value, color='red', linestyle='--',
            label=f'均值: {mean_value:.2f} dBm')

# 设置字体为宋体
plt.rcParams['font.sans-serif'] = ['SimSun']  # 设置全局字体为宋体
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题

# 设置标题和坐标轴标签
plt.title('RSRP数据分布直方图', fontsize=14, fontname='SimSun')
plt.xlabel('RSRP值 (dBm)', fontsize=12, fontname='SimSun')
plt.ylabel('频数', fontsize=12, fontname='SimSun')

# 设置纵轴最大刻度并留出顶部空间
ax = plt.gca()
ax.margins(y=0.2)  # 纵轴顶部留 20% 空间
ax.yaxis.set_major_locator(MaxNLocator(integer=True))  # 纵轴刻度设置为整数

# 设置横轴范围
plt.xlim(-80, -100)  # 横轴从 -80 到 -100，-80 在最右边

# 添加图例和外边框
plt.legend(loc='lower right', fontsize=10,
           frameon=True, edgecolor='black')  # 图例在右上角
ax.spines['top'].set_linewidth(1.5)  # 加粗上边框
ax.spines['bottom'].set_linewidth(1.5)  # 加粗下边框
ax.spines['left'].set_linewidth(1.5)  # 加粗左边框
ax.spines['right'].set_linewidth(1.5)  # 加粗右边框

# 在图像右上角加入均值和标准差
plt.text(0.95, 0.95, f'均值: {mean_value:.2f} dBm\n标准差: {std_value:.2f} dBm',
         transform=ax.transAxes, fontsize=10, fontname='SimSun',
         verticalalignment='top', horizontalalignment='right',
         bbox=dict(boxstyle="round", facecolor="white", edgecolor="black"))

# 调整布局
plt.tight_layout()

# 显示直方图
plt.show()


# 绘制箱线图
plt.figure(figsize=(6, 8))  # 设置图像大小
boxprops = dict(linewidth=1.5, color='#DB472A')  # 箱体样式，使用颜色 #DB472A
medianprops = dict(linewidth=1.5, color='black')  # 中位数线样式
whiskerprops = dict(linewidth=1.5, color='#DB472A')  # 触须样式
capprops = dict(linewidth=1.5, color='#DB472A')  # 端点样式
flierprops = dict(marker='o',  # 异常值样式
                  markerfacecolor='#DB472A',
                  markersize=5,
                  linestyle='none',
                  markeredgecolor='none'  # 新增边框颜色控制
                  )

plt.boxplot(df['平均RSRP'], vert=True, patch_artist=False,  # 纵向显示，箱体不填充
            boxprops=boxprops, medianprops=medianprops,
            whiskerprops=whiskerprops, capprops=capprops, flierprops=flierprops)


# 设置标题和坐标轴标签
plt.title('RSRP数据分布箱线图', fontsize=14, fontname='SimSun')  # 设置标题字体为宋体
plt.ylabel('RSRP值 (dBm)', fontsize=12, fontname='SimSun')  # 设置纵轴标签字体为宋体
plt.xticks([1], ['平均RSRP'], fontsize=10, fontname='SimSun')  # 设置横轴刻度字体为宋体

# 设置纵轴范围
plt.ylim(-100, -80)

# 添加外边框
ax = plt.gca()
ax.spines['top'].set_linewidth(1.5)
ax.spines['bottom'].set_linewidth(1.5)
ax.spines['left'].set_linewidth(1.5)
ax.spines['right'].set_linewidth(1.5)

# 调整布局
plt.tight_layout()

# 显示箱线图
plt.show()


# 写入 Excel 并添加统计指标
path = r"D:\工作\创新\QC\科创QC\方案细化\RSRP_测试报告.xlsx"
with pd.ExcelWriter(path) as writer:
    df.to_excel(writer, index=False, sheet_name='测量数据')

    stats = pd.DataFrame({
        'Max': [df['平均RSRP'].max()],
        'Min': [df['平均RSRP'].min()],
        '极差R': [df['平均RSRP'].max() - df['平均RSRP'].min()],
        '平均值X': [df['平均RSRP'].mean()],
        '标准差S': [df['平均RSRP'].std(ddof=1)]
    }, index=['统计值'])

    stats.to_excel(writer, sheet_name='测量数据',
                   startrow=len(df) + 2, startcol=0, header=True)  # 将统计值写在数据下方

数据检验

T 检验

import numpy as np
from scipy import stats

data1 = [-88.8, -93.1, -86.9, -89.5, -84.6, -88.4, -91.1, -89.5, -89.2, -91.1, -88.9, -android89.6, -89.6, -89.3, -91, -88, -91.9, -87.7, -85.4, -88.4, -86, -90.3, -90.6, -85.9, -86.3, -90.1, -92.1, -88.6, -90, -92.3]
data2 = [-82.1, -85.2, -82.1, -87.6, -82.5, -86.7, -84, -84.1, -84.7, -83.3, -86.6, -87.2, -79.7, -84.8, -85.2, -81.4, -83.6, -84.3, -85.7, -87.7, -86.3, -86.2, -87.7, -84.2, -86.9, -84.2, -85.4, -85.7, -87.1, -82.9]

# 方差齐性检验
levene_test = stats.levene(data1, data2)
print("Levene检验结果：统计量=%.4f, p值=%.4f" % (levene_test.statistic, levene_test.pvalue))

# 根据方差齐性结果选择equal_var参数
if levene_test.pvalue > 0.05:
    equal_var = True
else:
    equal_var = False

# 进行独立样本T检验
t_stat, p_value = stats.ttest_ind(data1, data2, equal_var=equal_var)
print("\n独立样本T检验结果：")
print("t统计量 =", t_stat)
print("p值 =", p_value)

# 计算自由度（如果是Welch检验）
if not equal_var:
    n1 = len(data1)
    n2 = len(data2)
    var1 = np.var(data1, ddof=1)
    var2 = np.var(data2, ddof=1)
    df = (var1/n1 + var2/n2) **2 / ((var1/n1)** 2/(n1-1) + (var2/n2)**2/(n2-1))
    print("自由度 =", df)
else:
    df = len(data1) + len(data2) - 2
    print("自由度 =", df)
    
def cohen_d(data1, data2):
    n1, n2 = len(data1), len(data2)
    var1 = np.var(data1, ddof=1)  # 无偏估计
    var2 = np.var(data2, ddof=1)
    pooled_std = np.sqrt( ((n1-1)*var1 + (n2-1)*var2) / (n1+n2-2) )
    return abs( (np.mean(data1)-np.mean(data2)) / pooled_std )

# 使用数据计算
d = cohen_d(data1, data2)
print(f"Cohen's d = {d:.2f}")  # 输出：Cohen's d = 2.15

ANova

对四个数据做ANOVA 分为四步 ：正态性判断能不能用，方差齐性判断用哪种、ANOVA看明显不明显、事后检验看哪两组最明显。

import numpy as np
from scipy import stats
from statsmodels.stats.multicomp import pairwise_tukeyhsd

# 用户数据
data1 = [17.1,14.4,15.6,16.4,14.3,15.5,19.3,17.4,16.2,15.3,17.8,11.4,13.8,17.5,16.5,16.1,16.8,11.7,17.8,18.2,17.1,14.1,17.3,17.8,16,14.7,16.1,16.2,15.3,13.8]
data2 = [13.9,16.7,18.5,15.1,12.1,13.3,12.4,15.5,15.9,15,14,15.3,14.6,14.4,16,18.2,16.8,15.9,14.4,15.1,16.2,14.1,14.2,16,13.1,12.9,15.8,18.4,16.5,16.4]
data3 = [13.4,17.9,19.2,15.1,16.3,16.1,13.7,17.3,14.9,13.1,14.8,15.8,14.8,11.7,16.2,13.2,17.5,16.6,17.2,14.8,15.9,15.7,16.5,15.2,16.8,13.5,15.1,14.4,13.3,14.3]
data4 = Data4 = [17, 19.7, 16.5, 18, 18.5, 17.2, 20, 18.4, 16.7, 18.2, 18.2, 16.1, 16.3, 19.6, 17, 17.4, 21.2, 18.3, 18.2, 16.5, 17.9, 13.2, 14.4, 13.9, 18.9, 16.6, 17.7, 18.7, 15.9, 16]

# 正态性检验（Shapiro-Wilk）
for i, data in enumerate([data1, data2, data3,android data4], 1):
    stat, p = stats.shapiro(data)
    print(f"Data{i}正态性检验: W={stat:.3f}, p={p:.3f}")

# 方差齐性检验（Levene）
levene_stat, levene_p = stats.levene(data1, data2, data3, data4)
print(f"\nLevene方差齐性检验：F={levene_stat:.2f}, p={levene_p:.4f}")

# 单因素ANOVA
f_stat, p_value = stats.f_oneway(data1, data2, data3, data4)
print(f"\n单因素ANOVA结果：F({3},{116})={f_stat:.2f}, p={p_value:.4f}")

# 效应量计算（Eta squared）
total = np.concatenate([data1, data2, data3, data4])
ss_total = np.var(total, ddof=1) * (len(total)-1)
eta_sq = (f_stat * 3) / (f_stat * 3 + 116)  # 公式： = (F * df_between) / (F * df_between + df_within)
print(f"效应量 = {eta_sq:.3f}")

# 事后检验（Tukey HSD）
tukey = pairwise_tukeyhsd(
    endog=np.concatenate([data1, data2, data3, data4]),
    groups=np.array(['Data1']*30 + ['Data2']*30 + ['Data3']*30 + ['Data4']*30),
    alpha=0.05
)
print("\nTukey HSD事后检验结果：")
print(tukey.summary())

二、动态图表

使用有代码开源动态图表网站，寻找合适的模板，将图表和对应的代码输入大模型，然后提出修改意见和生成代码。

按优先顺序推荐如下

1、apache echarts的示例

图表好看、类型齐全、提供代码 https://echarts.apache.org/examples/zh/index.html#chart-type-line

2、pyercharts的基础图表

图表一般、类型齐全、提供代码 https://05x-docs.pyecharts.org/#/zh-cn/charts_base

3、镝数图标

图表好看、类型齐全、不提供代码，仅能参考 https://dycharts.com/appv2/#/pages/home/chart-template

三、画图的美化

给大模型提供美化库，让他使用特定的美化库的美化模板进行绘图。

1、Matplotx

主要用在深色主题的绘图中，特别是用在黑色或者蓝色的科技感演讲PPT中。

主题如下，其中Dracula主题非常流行。

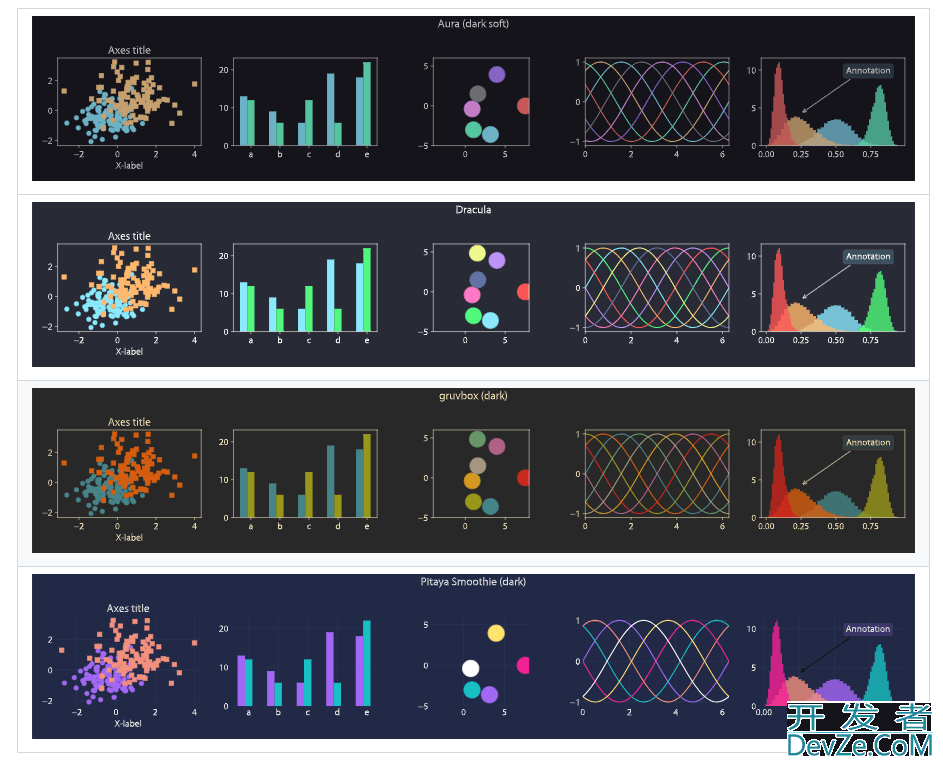
2、案例图形

1、阴影雷达图

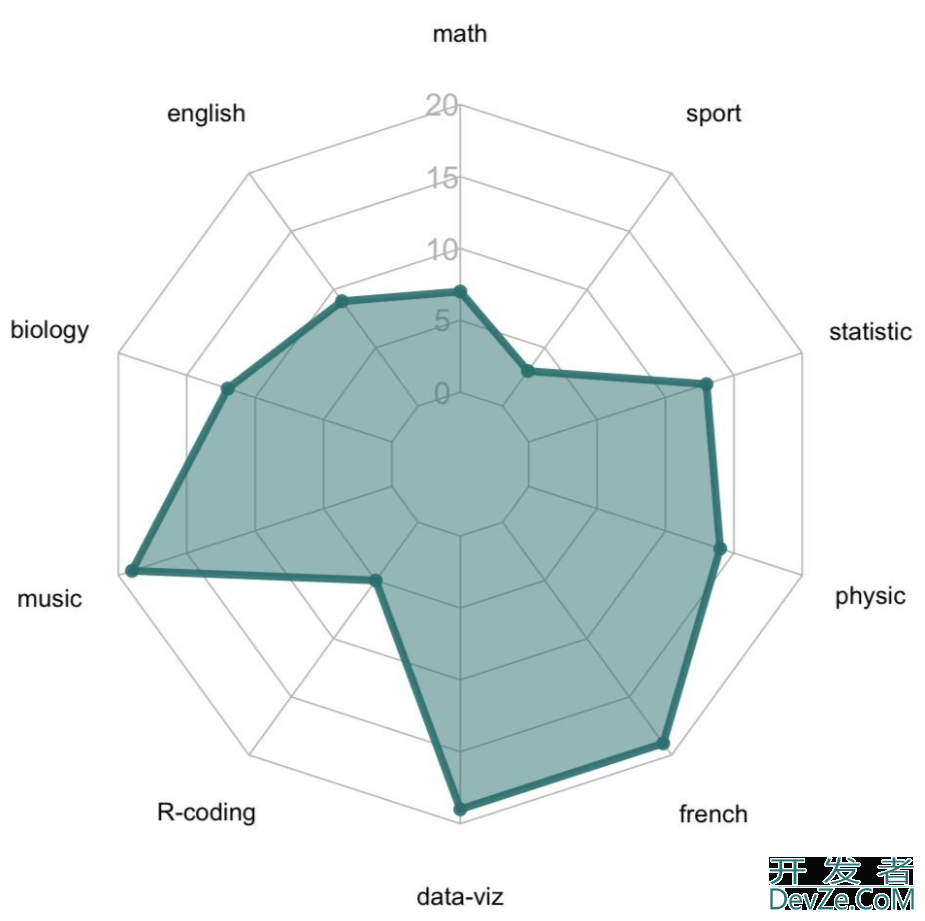
3、其他工具

数据专列表

def convert_to_list(input_data):
    """
    将一列数字转换为 Python 列表。
    
    参数:
        input_data (str): 包含一列数字的字符串，每行一个数字。
    
    返回:
        list: 转换后的 Python 列表。
    """
    # 按行分割输入数据
    lines = input_data.strip().splitlines()
    
    # 将每一行的数字转换为浮点数或整数
    data_list = []
    for line in lines:
        stripped_line = line.strip()
        if "." in stripped_line:  # 判断是否为浮点数
            data_list.append(float(stripped_line))
        else:
            data_list.append(int(stripped_line))
    
    return data_list


# 示例输入数据
input_data = """
17

"""

# 调用函数并打印结果
data_list = convert_to_list(input_data)
print(data_list)

以上就是Python使用大语言模型进行图表可视化的详细内容，更多关于Python大模型图表可视化的资料请关注编程客栈(www.devze.com)其它相关文章！