C语言之浮点数的表示与储存方式

目录

• 1. 二进制小数
• 1.1 十进制小数的表示方法
• 1.2 二进制小数的表示方法
• 2. IEEE浮点表示
• 2.1 IEEE浮点标准
• 2.2 单精度和双精度浮点数的封装形式
• 2.3 浮点数的数值分类
• 2.3.1 规格化的值 (Normalized Values)
• 2.3.2 非规格化的值 (Denormalized Values)
• 2.3.3 特殊值 (Special Values)
• 3. 数字示例
• 4. 舍入
• 5. 浮点运算
• 6. C语言中的浮点数
• 总结

1. 二进制小数

1.1 十进制小数的表示方法

理解浮点数的第一步是考虑含有小数值的十进制数字

先来看一下十进制数字的表示法：

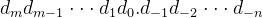
其中每个十进制数

的取值范围是0~9。这个表达描述的数值

的定义如下：

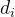
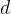
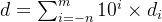
数字权的定义与十进制小数点符号( ‘.’ ) 相关，这意味着小数点左边的数字的权是10的正幂，得到整数值，而小数点右边的数字的权是10的负幂，得到小数值。例如十进制数12. 34表示数http://www.devze.com字

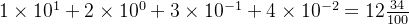
1.2 二进制小数的表示方法

类比十进制数，二进制表示小数可以用如下表示法表示，

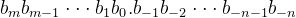
以图片表示为：

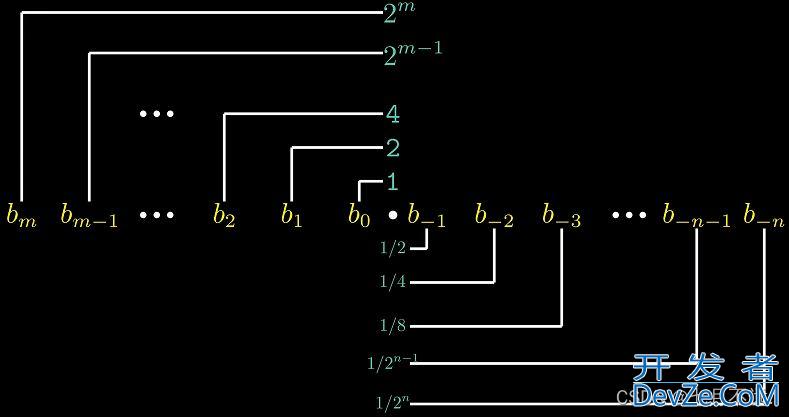
其中

的取值范围是0和1。这个表达描述的数值

的定义如下：

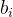
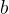
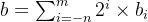
符号 ‘ . ’ 现在变为了二进制的点，点左边的位的权是2的正幂，点右边的位的权是2的负幂。例如，二进制数101.11表示数字

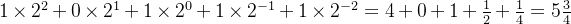
2. IEEE浮点表示

2.1 IEEE浮点标准

上一节提到的定点表示法并不能很有效地表示非常大的数字。IEEE(电气和电子工程师协会)浮点标准用如下的形式来表示一个数：

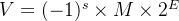
在这个式子中设计三个变量，s, M以及E

符号 (sign) : s决定这数是负数 (s = 1) 还是正数 (s = 0)尾数 (ignificand) : M是一个二进制小数阶码 (exponent): E的作用是对浮点数加权，这个权重是2的E次幂(可能是负数)

例如：

5.0 化为二进制小数

，由于 5.0 为正数，因此 s = 0，M = 1.01，E = 2

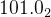
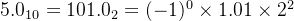
这种标准将浮点数封装成一种似乎很难理解的形式来存储，但其实是相当优雅的。

2.2 单精度和双精度浮点数的封装形式

在C语言中，浮点数分为单精度浮点数 float 和双精度浮点数 double，其中float在内存中占4个字节，32个比特位；double在内存中占8个字节，64个比特位。

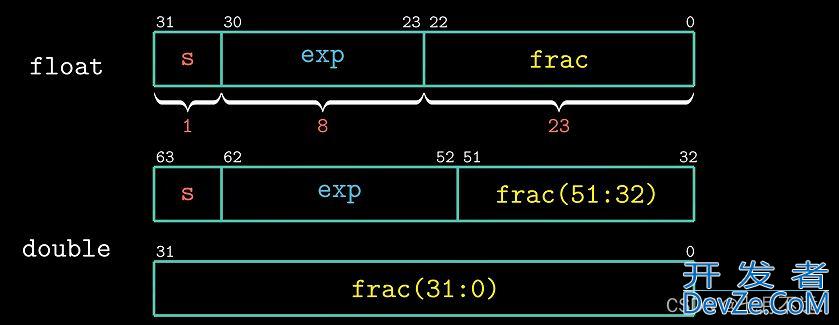
不管是 float 还是 double ，它们都被分为三个字段，分别用来表示符号位s，阶码字段exp和编码尾数frac。这三个字段与上述的符号s，尾数M，阶码E一一对应，但并非将s,M,E直接存入内存，而是根据浮点数的不同数值类型按照不同的规则进行编码。

2.3 浮点数的数值分类

根据阶码的不同，浮点数的数值可以分为三类：

• 规格化的值 (Normalized Values)
• 非规格化的值 (Denormalized Values)
• 特殊值 (Special Values)

exp的值决定了这个数属于上面类型中的哪一种，以float类型为例：

2.3.1 规格化的值 (Normalized Values)

当阶码域不全为0并且不全为1时，表示该数值为规格化的值

当阶码字段不全为0时，表示该数值为非规格化的值。这是一种最普遍的情况，大多数浮点数都属于这类。比如上一小节的5.0

对于规格化的值，在得到s, E, M之后还需要进行一些处理才能放进内存：

规则1：

• 前面已经提到，E是阶码并且可以表示负值，存放在exp字段，但是E在标准中为无符号数，这说明它不能表示负数且可表示的范围为0~255。那么对于E为负值的情况如何处理呢？
• 这里引入偏置 (Bias) 的概念。
• IEEE 754规定，存入内存时E的真实值必须再加上一个中间数，对于8位的E，这个中间数是127；对于11位的E，这个中间数是1023。这里的127和1023就是Bias。也就是说，阶码的值是 E= exp - Bias
• 例如：2^10的E是10，所以保存成32位浮点数时，必须保存成10+127=137，即10001001。此时内存中的exp中存的是10001001。

规则2

• 同样的，M存放在小数字段 f 中，我们知道，当一个小数化为二进制小数后所得到的M总是一个介于1~2之间的值，形式为1. xxxxx
• 因此在存数据时，考虑省略小数点前面的1（取数据的时候可以直接在前面添上），可以节省一位的存储空间，能让小数点后的数据多保存一位，提高数据的精度。
• 例如，M=1.01101，存到 f 中去的数据为01101，M = 1 + f

到这里我们可以解决 5.0 这样一个规格化的值的存放问题了：

我们知道，对于5.0来说，s = 0，M = 1.01，E = 2，

根据以上规则，在内存中，符号位字段s = 0，阶码字段exp = E + 127 = 129 = 10000001，编码尾数f = 01000000000000000000000（不够23位要在后面补0）

结合来看：

0 10000001 01000000000000000000000，化为十六进制为40 a0 00 00

在小端机器上的结果为：

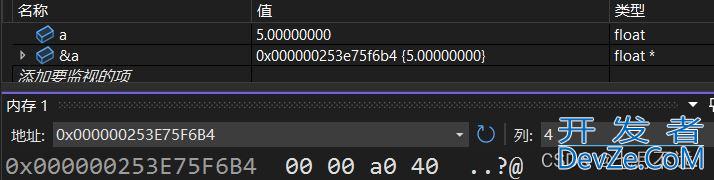
2.3.2 非规格化的值 (Denormalized Values)

当阶码域为全0时, 所表示的数是非规格化的值

在这种情况下，规则又有所不同：

规则1

• 当exp为全0时，此时的E = 1- Bias，也就是说1-127（或者1-1023）即为真实值
• 补充：使阶码值为 1-Bias 仍而不是简单的 -Bias 似乎是违反直觉的。在后面我们会知道，这种方式提供了一种从非规格化值平滑转换到规格化值的方法

规则2

• 有效数字M不再加上第一位的1，而是还原为0.xxxxxx的小数，即M = f ，也就是小数字段的值, 不包含隐含的开头的1
• 实际上，如M = 1.01101，在exp = 00000000时，存进去的是101101而不是01101

非规格化数有两个用途：

• 首先，它们提供了一种表示数值0 的方法，因为使用规格化数，我们必须总是M>= 1，因此我们就不能表示0.0
• 其次，非规格化数的另外一个功能是表示那些非常接近于 0.0 的数。它们提供了一种属性，称为逐渐溢出(gradualunder flow) ，其中，可能的数值分布均匀地接近于0.0

2.3.3 特殊值 (Special Values)

当阶码域为全1时, 所表示的数是特殊值

特殊值可分为两种：

1. 当小数域全为0 时，得到的值表示无穷，当 s = 0 时，是+∞, 或者当 s = 1时，是 -∞

2.当小数域为非零时, 结果值被称为 “NaN”(Not a Number)。一些运算的结果不能是实数或无穷, 就会返回这样的NaN值

3. 数字示例

为了更加直观地理解，我们用一个8位浮点数的例子，假定符号位 s 的长度为1，阶码字段的长度为4，小数字段的长度为3：

对于非规格数：

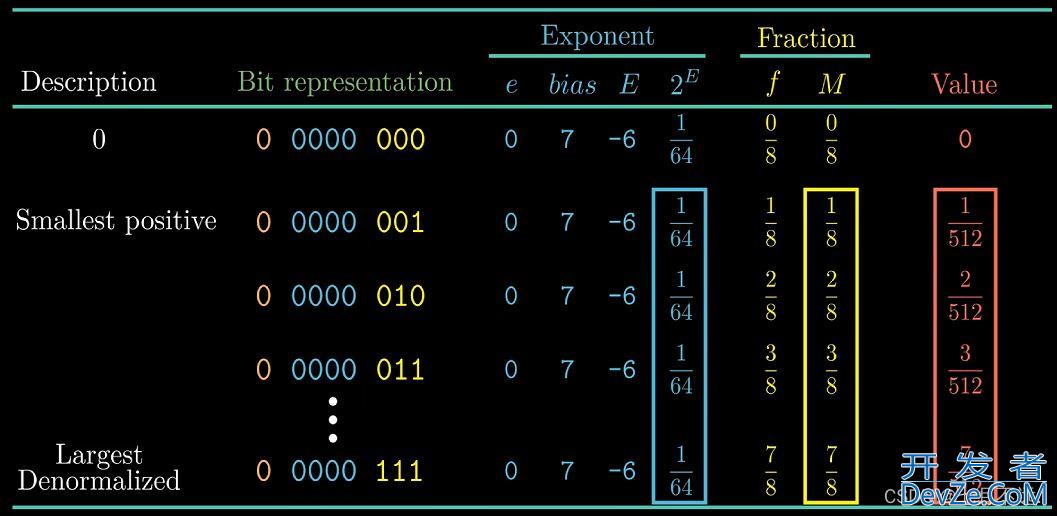
对于规格数

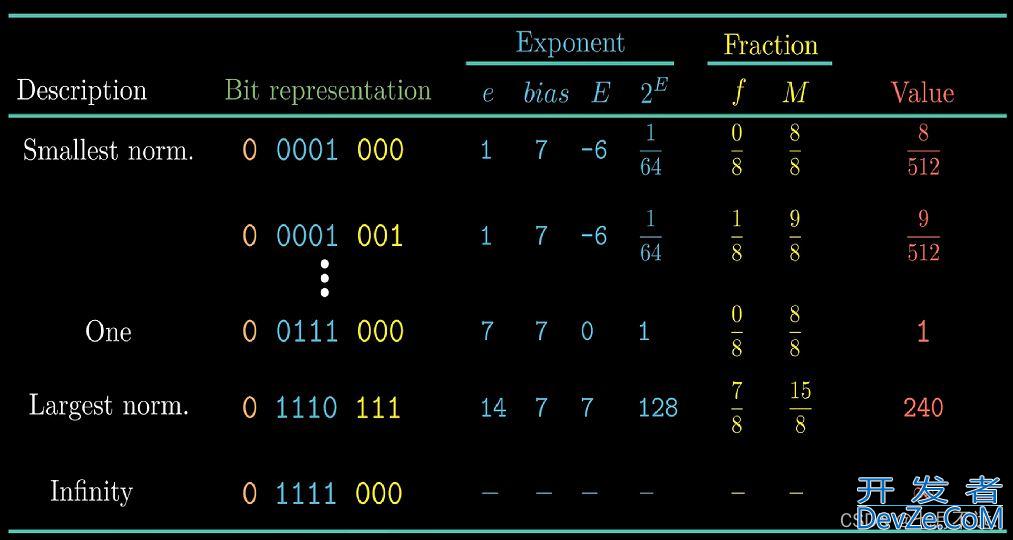
可以看到，从最大非规格数0 0000 111到最小规格数0 0001 000这样的过渡是很自然的，体现出了上编程客栈述IEEE标准的逻辑性与和谐的美感

4. 舍入

因为表示方法限制了浮点数的范围和精度, 所以浮点运算只能近似地表示实数运算

我们企图找到一个与值

最相近的值匹配值

来作为储存的值

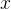
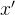
例如：

如果由于表示方法的限制，1.5这样一个值无法完全放在内存中，需要舍掉小数点后的值，那么舍入结果是1还是2呢❔

IEEE定义了四种舍入方式：

• 向偶数舍入
• 向零舍入
• 向上舍入
• 向下舍入

其中，向偶数编程客栈舍入(round - to - even)又被称为向最接近的值舍入(round - to - nearest)，是默认的方式，试图找到一个最接近的匹配值

向上和向下舍入很好理解，一个介于1~2之间的数如 1.5 向上舍入是2，向下舍入是1

向零舍入是指在在数轴上的数向 0 的方向进行舍入，比如 1.50 向零舍入会找到 1 和 2 之间更靠近0 的数 1 ，-1.50 向零舍入会找到 -1 和 -2 之间更靠近 0 的数 -1

向偶数舍入，指当一个数是两个可能结果的中间数时，它将数字向上或者向下舍入，使得结果的最低有效数字是偶数

比如1.50可以向1舍入，也可以向2舍入，并且正好是1和2的中间值，这时会默认向2(偶数)舍入；比如2.50可以向2舍入，也可以向3舍入，并且正好是2和3的中间值，这时同样会向2(偶数)舍入。

值得注意的是：

向偶数舍入只针对那些“中间值”。当值为1.49或1.51时，依旧舍入为 1 和 2

方式	1.40	1.60	1.50	2.50	-1.50
向偶数舍入	1	2	2	2	-2
向零舍入	1	1	1	2	-1
向上舍入	1	1	1	2	-2
向下舍入	2	2	2	3	-1

为什么要使用向偶数舍入呢？

使用其他三种舍入方法，在一组数据中很容易引入平均值的统计偏差 ，当1.50 1.60 1.70这样一组数据都使用向上舍入，结果是2 2 2，平均值会偏大

向偶数舍入在大多数现实情况中避免了这种统计偏差。在50%的时间里，它将向上舍入，而在50%的时间里，它将向下舍入

对二进制的浮点数舍入同样遵循向偶数舍入的原则，并将 0 视为偶数，1 视为奇数

例如：

10.11100 ，当舍入需要精确到小数点后两位时， 后三位100代表

，正好是中间值，因此向偶数舍入为11.00

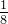
5. 浮点运算

考虑下面几个式子：

• (1) (3.14 + 1e10) - 1e10 = 0www.devze.com.0
• (2) 3.14 + (1e10 - 1e10) = 3.14
• (3) (1e20 * 1e20) * 1e-20 = +∞
• (4) 1e20 * (1e20 * 1e-20) = 1e20
• (5) 1e20 * (1e20 - 1e20) = 0.0
• (6) 1e20*1e20 - 1e20*1e20 = NaN

• (1)(2)中，3.14 + 1e10对结果进行了舍入，值3.14会丢失，因此对于浮点数的加法不具有结合性
• (3)(4)中，由于计算结果可能溢出或舍入，因此浮点数的乘法也不具有结合性
• (5)(6)中，在单精度浮点数时结果不同，说明浮点数乘法不具有分配性

6. C语言中的浮点数

所有的C语言版本提供了两种不同的浮点数据类型: float 和 double

当int ，float，double不同数据类型之间进行强制类型转换时，得到的结果可能会超出我们的预期，程序改变数值和位模式的原则如下( 假设int是32位的) :

• 从 int 转换成 float，数字不会溢出，但是可能被舍入
• 从 int 或 float 转换成 double，因为double有更高的精度，所以能够保留精确的数值
• 从 double 转换成 float ，因为范围要小一些，所以值可能溢出成 +∞ 或 -∞。另外，由于精确度较小，它还可能被舍入
• 从 float 或者 double 转换成int，值将会向零舍入。例如，1.android999将被转换成1，而-1.999将被转换成 -1。进一步来说，值可能会溢出

总结

以上为个人经验，希望能给大家一个参考，也希望大家多多支持编程客栈(www.devze.com)。