Java中的弗洛伊德(Floyd)算法
弗洛伊德Floyd算法
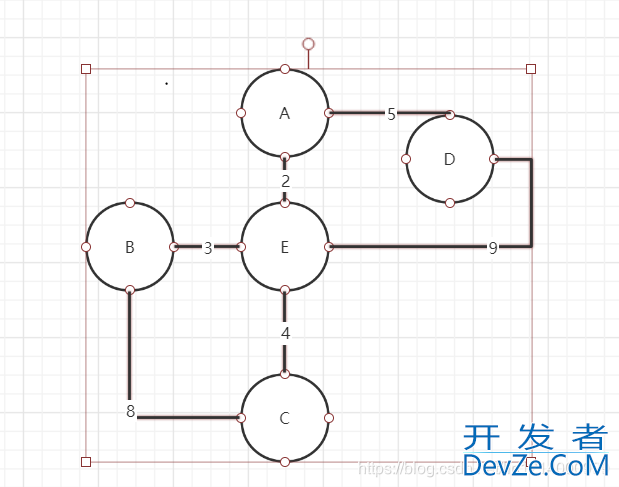
Floyd算法又称为插点法,是一种利用动态规划的思想寻找给定的加权图中多源点之间最短路径的算法,与Dijkstra算法类似。
该算法名称以创始人之一、1978年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德命名。
Dijkstra算法是求一个出发节点到其他各节点的最短距离,而Floyd算法是求每个节点到其他个节点的最短距离
完整Java代码:
package com.yg.algorithm;/*
@author Mu_Mu
@date 2020/3/23 9:56
*/
public class FloydAlgorithm {
private static final int MAX=10000;
public static void main(String[] args) {
char[] vertexs = android{'A', 'B', 'C', 'D', 'E'};
int[][] matrix = {{0, MAX, MAX, 5, 2}, {MAX, 0, 8, MAX, 3}
, {MAX, 8, 0, MAX, 4}, {5, MAX, MAX, 0, 9},{2,3,4,9,0}};
FGraph fGraph = new FGraph(vertexs, matrix);
编程客栈fGraph.floyd();
fGraph.show();
}
}
class FGraph {
private char[]vertexs;//存放顶点
private int [][]dis;//每个顶点之间的距离
private int[][]pre;//存放前驱顶点
public FGraph(char[] vertexs, int[][] dis) {
this.vertexs = vertexs;
this.dis = dis;
pre=new int [vertexs.length][vertexs.length];
//初始化前驱顶点
for (int i = 0; i < vertexs.length; i++) {
for (int j = 0; j < vertexs.length; j++) {
pre[i][j]=i;
}
}
}
//弗洛伊德算法
public void floyd() {
int len=0;
//i,遍历中间顶点,3层循环的意义就是j通过i到k
for (int i = 0; i < vertexs.length; i++) {
//j代表出发节点
for (int j = 0; j < vertexs.length; j++) {
python //k代表终点顶点
for (int k = 0; k < vertexs.length; k++) {
//记录j通过i到k的距离
len=dis[j][i]+dis[i][k];
//比较j通过i到k的距离是否小于j直接到k的距离
if (len < dis[j][k]) {
dis[j][k]=len;
pre[j][k]=prephp[i][k];
}
}
}
}
}
//打印图
public void show() {
for (int i = 0; i <编程; vertexs.length; i++) {
//打印前驱顶点
for (int j = 0; j < vertexs.length; j++) {
System.out.print(vertexs[pre[i][j]]+" ");
}
System.out.println();
//打印顶点之间的距离
for (int k = 0; k < vertexs.length; k++) {
System.out.print(vertexs[i]+"到"+vertexs[k]+"的距离为:"+dis[i][k]+" ");
}
System.out.println();
}
}
}
到此这篇关于Java中的弗洛伊德(Floyd)算法的文章就介绍到这了,更多相关弗洛伊德Floyd算法内容请搜索编程客栈(www.devze.com)以前的文章或继续浏览下面的相关文章希望大家以后多多支持编程客栈(www.devze.com)!





 加载中,请稍侯......
加载中,请稍侯......
精彩评论