利用python实现3种梯度下降算法

目录

• 全量梯度下降
• 随机梯度下降
• 小批量梯度下降
• 三种梯度下降区别和优缺点

全量梯度下降

BATch Gradient Descent

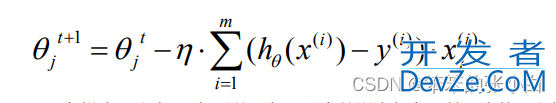
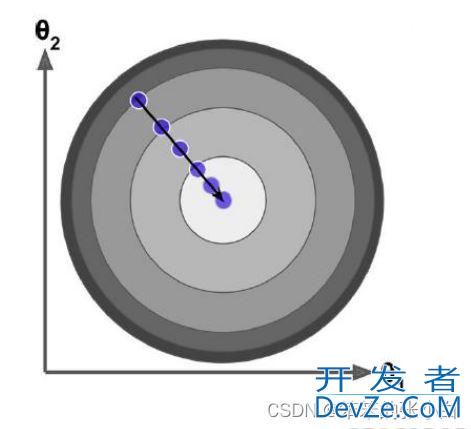
在梯度下降中，对于θ的更新，所有的样本都有贡献，也就是参与调整θ。其计算得到 的是一个标准梯度。因而理论上来说一次更新的幅度是比较大的。如果样本不多的情况下， 当然是这样收敛的速度会更快啦。全量梯度下降每次学习都使用整个训练集，因此其优点在 于每次更新都会朝着正确的方向进行，最后能够保证收敛于极值点(凸函数收敛于全局极值 点，非凸函数可能会收敛于局部极值点)，但是其缺点在于每次学习时间过长，并且如果训 练集很大以至于需要消耗大量的内存，并且全量梯度下降不能进行在线模型参数更新。

代码实现：

import numpy as np
 
# 创建数据集X，y
np.random.seed(1)
X = np.random.rand(100, 1)
y = 4 + 3*X + np.random.randn(100, 1)
X_b = np.c_[np.ones((100, 1)), X]
 
# 创建超参数
n_iterations = 10000
t0, t1 = 5, 500
 
# 定编程义一个函数来动态调整学习率
def learning_rate_schedule(t):
    return t0/(t+t1)
 
# 1,初始化, W0...Wn，标准正太分布创建W
theta = np.random.randn(2, 1)
# 4,判断是否收敛，一般不会去设定阈值，而是直接采用设置相对大的迭代次数保证可以收敛
for i in range(n_iterations):
    # 2,求梯度，计算gradient
    gradients = X_b.T.dot(X_b.dot(theta)-y)
    # 3,应用梯度下降法的公式去调整值 t+1=t-*gradient
    learning_rate = learning_rate_schedule(i)
    theta = theta - learning_rate * gradients
print(theta)

[[4.23695725]
 [2.68492509]]

随机梯度下降

Stochastic Gradient Descent

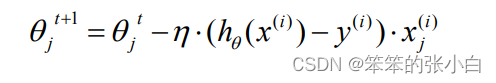
梯度下降算法每次从训练集中随机选择一个样本来进行学习。批量梯度下降算法每次都 会使用全部训练样本，因此这些计算是冗余的，因为每次都使用完全相同的样本集。而随机 梯度下降算法每次只随机选择一个样本来更新模型参数，因此每次的学习是非常快速的，并 且可以进行在线更新。随机梯度下降最大的缺点在于每次更新可能并不会按照正确的方向进 行，因此可以带来优化波动(扰动)。

不过从另一个方面来看，随机梯度下降所带来的波动有个好处就是，对于类似盆地区域 （即很多局部极小值点）那么这个波动的特点可能会使得优化的方向从当前的局部极小值点 跳到另一个更好的局部极小值点，这样便可能对于非凸函数，最终收敛于一个较好的局部极 值点，甚至全局极值点。由于波动，因此会使得迭代次数（学习次数）增多，即收敛速度变 慢。不过最终其会和全量梯度下降算法一样，具有相同的收敛编程客栈性，即凸函数收敛于全局极值 点，非凸损失函数收敛于局部极值点。       

代码实现：

import numpy as np
 
# 创建数据集
X = 2*np.random.rand(100, 1)
y = 4 + 3*X + np.random.randn(100, 1)
X_b = np.c_[np.ones((100, 1)), Xandroid]
# 创建超参数
n_epochs = 10000
m = 100
t0, t1 = 5, 500
 
# 定义一个函数来调整学习率
def learning_rate_schedule(t):
    return t0/(t+t1)
 
theta = np.random.randn(2, 1)
for epoch in range(n_epochs):
    # 在双层for循环之间，每个轮次开始分批次迭代之前打乱数据索引顺序
    arr = np.arange(len(X_b))
    np.random.shuffle(arr)
    X_b = X_b[arr]
    y = y[arr]
    for i in range(m):
        xi = X_b[i:i+1]
        yi = y[i:i+1]
        gradients = xi.T.dot(xi.dot(theta)-yi)
        learning_rate = learning_rate_schedule(epoch*m + i)
        theta = theta - learning_rate * gradients
 
print(theta)

[[3.91306085]
 [3.16087742]]

小批量梯度下降

Mini-Batch Gradient Descent

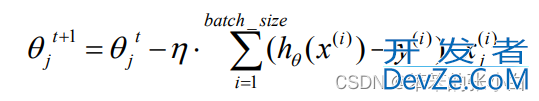
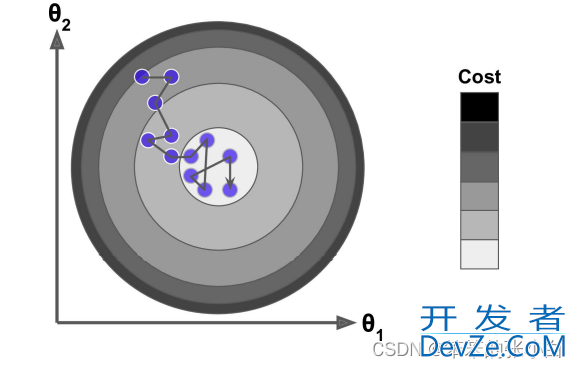
Mini-batch 梯度下降综合了 batch 梯度下降与 stochastic 梯度下降，在每次更新速 度与更新次数中间取得一个平衡，其每次更新从训练集中随机选择 batch_size，batch_size < m 个样本进行学习。相对于随机梯度下降算法，小批量梯度下降算法降低了收敛波动性， 即降低了参数更新的方差，使得更新更加稳定。相对于全量梯度下降，其提高了每次学习的速度。并且其不用担心内存瓶颈从而可以利用矩阵运算进行高效计算。一般而言每次更新随 机选择[50,256]个样本进行学习，但是也要根据具体问题而选择，实践中可以进行多次试验， 选择一个更新速度与更次次数都较适合的样本数。

代码实现：

import numpy as np
 
# 创建数据集X，y
X = 2*np.random.rand(100, 1)
y = 4 + 3*X + np.random.randn(100, 1)
X_b = np.c_[np.ones((100, 1)), X]
 
# 创建超参数
t0, t1 = 5, 500
 
# 定义一个函数来动态调整学习率
def learning_rate_schedule(t):
    return t0/(t+t1)
 
n_epochs = 100000
m = 100
batch_size = 10
num_batches = int(m / batch_size)
 
theta = np.random.randn(2, 1)
for epoch in range(n_epochs):
    arr = np.arange(len(X_b))
    np.random.shuffle(arr)
    X_b = X_b[arr]
    y = y[arr]
    for i in range(num_batches):
        x_batch = X_b[i*batch_size: i*batch_size + batch_size]
        y_batch = y[i*batch_size: i*batch_size + batch_size]
        gradients = x_batch.T.dot(x_batch.dot(theta)-y_batch)
        learning_rate = learning_rate_schedule(epoch * m + i)
        theta = theta - learning_rate*gradients
 
prinpythont(theta)

[[3.91630905]
 [2.95252566]]

三种梯度下降区别和优缺点

在讲三种梯度下降区别之前，我们先来总结一下梯度下降法的步骤：

1. 瞎蒙，Random 随机θ，随机一组数值 W0…Wn

2. 求梯度，为什么是梯度？因为梯度代表曲线某点上的切线的斜率，沿着切线往下下降就 相当于沿着坡度最陡峭的方向下降

3. if g0, theta 往小调

4. 判断是否收敛 convergence，如果收js敛跳出迭代，如果没有达到收敛，回第 2 步继续 四步骤对应计算方式：

a. np.random.rand()或者 np.random.randn()

b. i w j gradient = (h (x) - y)× x

c. Wi t+1 =Wi t -h ×gradient i

d. 判断收敛这里使用 g=0 其实并不合理，因为当损失函数是非凸函数的话 g=0 有可能是 极大值对吗！所以其实我们判断 loss 的下降收益更合理，当随着迭代 loss 减小的幅度 即收益不再变化就可以认为停止在最低点，收敛！

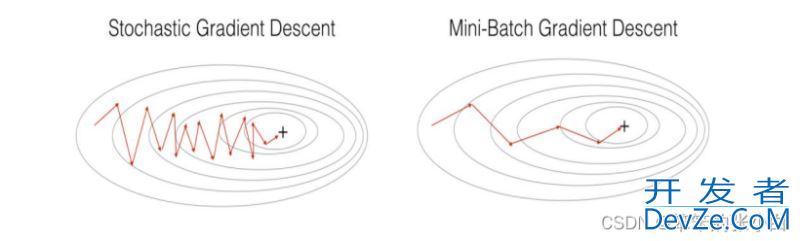
区别：其实三种梯度下降的区别仅在于第 2 步求梯度所用到的 X 数据集的样本数量不同！ 它们每次学习(更新模型参数)使用的样本个数，每次更新使用不同的样本会导致每次学习的 准确性和学习时间不同

以上就是利用python实现3种梯度下降算法的详细内容，更多关于python梯度下降算法的资料请关注编程客栈(www.devze.com)其它相关文章！