基于C#实现哈夫曼树算法
目录
- 一、概念
- 二、构建
- 三、代码
- 1、树节点
- 2、构建赫夫曼树(Build)
- 3、编码(Encode,Decode)
赫夫曼树又称最优二叉树,也就是带权路径最短的树,对于赫夫曼树,我想大家对它是非常的熟悉,也知道它的应用场景,但是有没有自己亲手写过,这个我就不清楚了,不管以前写没写,这一篇我们来玩一把。
一、概念
赫夫曼树里面有几个概念,也是非常简单的,先来看下面的图:
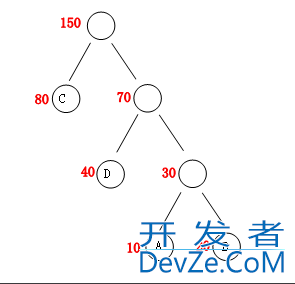
- 节点的权: 节点中红色部分就是权,在实际应用中,我们用“字符”出现的次数作为权。
- 路径长度:可以理解成该节点到根节点的层数,比如:“A”到根节点的路径长度为 3。
- 树的路径长度:各个叶子节点到根节点的路径长度总和,用 wpL 标记。
最后我们要讨论的的赫夫曼树也就是带权路径长度最小的一棵树。
二、构建
由于要使 WPL 最短,赫夫曼树的构建采用自低向上的方式,这里我们采用小根堆来存放当前需要构建的各个节点,我们的方式是每次从小根堆中取出最小的两个节点,合并后放入堆中,然后继续取两个最小的节点,一直到小根堆为空,最后我们采用自底向上构建的赫夫曼树也就完毕了。
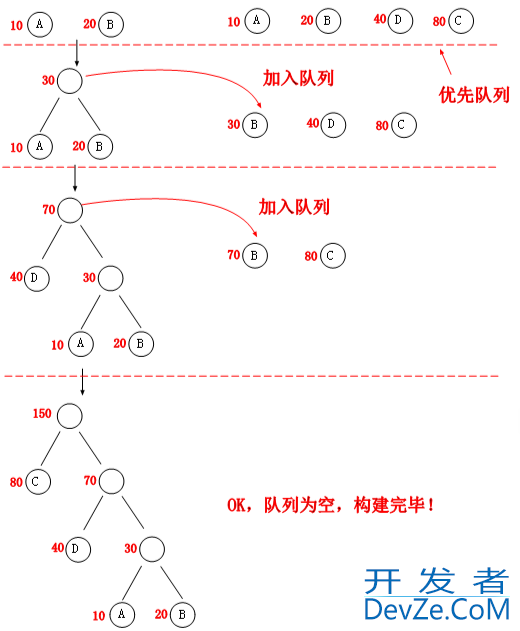
好了,赫夫曼树的典型应用就是在数据压缩方面,下面我们就要在赫夫曼树上面放入赫夫曼编码了,我们知道普通的 ASCII 码是采用等长编码的,即每个字符都采用 2 个字节,而赫夫曼编码的思想就是采用不等长的思路,权重高的字符靠近根节点,权重低的字符远离根节点,标记方式为左孩子“0”,右孩子“1”,如下图。
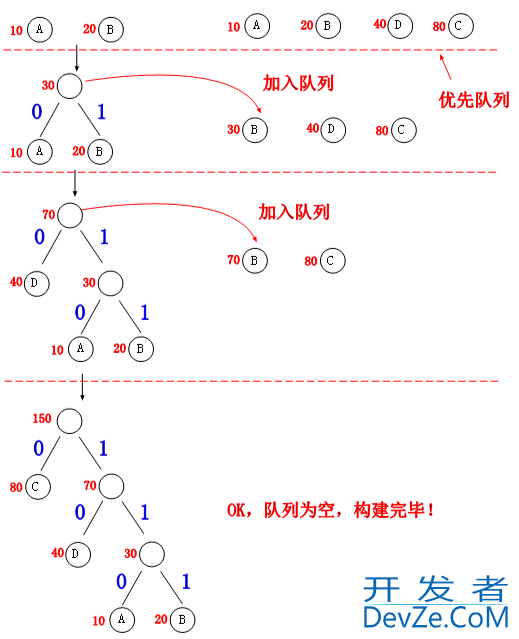
从图中我们可以看到各个字符的赫夫曼编码了,获取字符的编码采用从根往下的方式收集路径上的‘0,1’,如:
A:110。
B:111。C:0。D:10。
最后我们来比较他们的 WPL 的长度: ASCII 码=102+202+402+802=300
赫夫曼码=103+203+402+801=250
可以看到,赫夫曼码压缩了 50 个 0,1 字符。
三、代码
1、树节点
我们采用 7 元节点,其中 parent 方便我们在 DFS 的时候找到从叶子节点到根节点的路径上的赫夫曼编码。
#region 赫夫曼节点
/// <summary>
/// 赫夫曼节点
/// </summary>
public class Node
{
/// <summary>
/// 左孩子
/// </summary>
public Node left;
/// <summary>
/// 右孩子
/// </summary>
public Node right;
/// <summary>
/// 父节点
/// </summary>
public Node parent;
/// <summary>
/// 节点字符
/// </summary>
public char c;
/// <summary>
/// 节点权重
/// </summary>
public int weight;
//赫夫曼“0"or“1"
public char huffmancode;
/// <summary>
/// 标记是否为叶子节点
/// </summary>
public bool isLeaf;
}
#endregion
2、构建赫夫曼树(Build)
上面也说了,构建赫夫曼编码树我们采用小根堆的形式构建,构建完后,我们采用 DFS 的方式统计各个字符的编码,复杂度为 N*logN。
#region 构建赫夫曼树
/// <summary>
/// 构建赫夫曼树
/// </summary>
public void Build()
{
//构建
while (queue.Count() > 0)
{
//如果只有一个节点,则说明已经到根节点了
if (quRxirBRMlEeue.Count() == 1)
{
root = queue.Dequeue().t;
break;
}
//节点1
var node1 = queue.Dequeue();
//节点2
var node2 = queue.Dequeue();
//标记左孩子
node1.t.huffmancode = '0';
//标记为右孩子
node2.t.huffmancode = '1';
//判断当前节点是否为叶子节点,hufuman无度为1点节点(方便计算huffman编码)
if (node1.t.left == null)
node1.t.isLeaf = true;
if (node2.t.left == null)
node2.t.isLeaf = true;
//父节点
root = new Node();
root.left = node1.t;
root.right = node2.t;
root.weight = node1.t.weight + node2.t.weight;
//当前节点为根节点
node1.t.parent = node2.t.parent = root;
//将当前节点的父节点入队列
queue.Eequeue(root, root.weight);
}
//深度优先统计各个字符的编码
DFS(root);
}
#endregion
3、编码(Encode,Decode)
树构建起来后,我会用字典来保存字符和”赫夫曼编码“的对应表,然后拿着明文或者密文对着编码表翻译就行了, 复杂度 O(N)。
#region 赫夫曼编码
/// <summary>
/// 赫夫曼编码
/// </summary>
/// <returns></returns>
public string Encode()
{
StringBuilder sb = new StringBuilder();
foreach (var item in word)
{
sb.Append(huffmanEncode[item]);
}
return sb.ToString();
}
#endregion
#region 赫夫曼解码
/// <summary>
/// 赫夫曼解码
/// </summary>
/// <returns></returns>
public string Decode(string str)
{
StringBuilder decode = new StringBuilder();
string temp = string.Empty;
for (int i = 0; i < str.Length; i++)
{
temp += str[i].ToString();
//如果包含 O(N)时间
if (huffmanDecode.ContainsKey(temp))
{
decode.Append(huffmanDecode[temp]);
temp = string.Empty;
}
}
return decode.ToString();
}
#endregion
最后我们做个例子,压缩 9M 的文件,看看到底能压缩多少?
public static void Main()
{
StringBuilder sb = new StringBuilder();
for (int i = 0; i < 1 * 10000; i++)
{
sb.Append("人民网北京12月8日电 (记者 宋心蕊) 北京时间8日晚的央视《新闻联播》节目出现了直播失误。上一条新闻尚未播放完毕时,播就将画面切换回了演播间,主播李梓萌开始播报下一条新闻,导致两条新闻出现了“混音”播出。央视新闻官方微博账号在21点09分发布了一条致歉微博:【致歉】今晚《新闻联播》因导播员口令失误,导致画面切换错误,特此向观众朋友表示歉意。央视特约评论员杨禹在个人微博中写道:今晚《新闻联播》出了个切换错误,@央视新闻 及时做了诚恳道歉。联播一直奉行“金标准”,压力源自全社会的高要求。其实报纸亦都有“勘误”一栏,坦诚纠错与道歉。《新闻联播》是中国影响力最大的电视新闻节目。它有不可替代的符号感,它有失误,更有悄然的进步。新的改进正在或即将发生,不妨期待");
}
File.WriteAllText(Environment.CurrentDirectory + "//1.txt", sb.ToString());
Huffman huffman = new Huffman(sb.ToString());
Stopwatch watch = Stopwatch.StartNew();
huffman.Build();
watch.Stop();
Console.WriteLine("构建赫夫曼树耗费:{0}", watch.ElapsedMilliseconds);
//将8位二进制转化为ascII码
var s = huffman.Encode();
var remain = s.Length % 8;
List<char> list = new List<char>();
var start = 0;
for (int i = 8; i < s.Length; i = i + 8)
{
list.Add((char)Convert.ToInt32(s.Substring(i - 8, 8), 2));
start = i;
}
var result = new String(list.ToArray());
//当字符编码不足8位时, 用‘艹'来标记,然后拿出'擦‘以后的所有0,1即可
result += "艹" + s.Substring(start);
File.WriteAllText(Environment.CurrentDirectory + "//2.txt", result);
Console.WriteLine("压缩完毕!");
Console.Read();
//解码
var str = File.ReadAllText(Environment.CurrentDirectory + "//2.txt");
sb.Clear();
for (int i = 0; i < str.Length; i++)
{
int ua = (int)str[i];
//说明已经取完毕了 用'艹'来做标记
if (ua == 33401)
sb.Append(str.Substring(i));
else
sb.Append(Convert.ToString(ua, 2).PadLeft(8, '0'));
}
var sss = huffman.Decode(sb.ToString());
Console.Read();
}
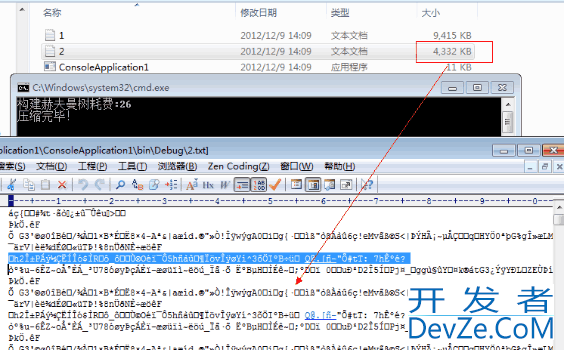
看看,将 9M 的文件压缩到了 4M。
主程序:
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Diagnostics;
using System.Threading;
using System.IO;
namespace ConsoleApplication2
{
public class Program
{
public static void Main()
{
StringBuilder sb = new StringBuilder();
for (int i = 0; i < 1 * 10000; i++)
{
sb.Append("人民网北京12月8日电 (记者 宋心蕊) 北京时间8日晚的央视《新闻联播》节目出现了直播失误。上一条新闻尚未播放完毕时,播就将画面切换回了演播间,主播李梓萌开始播报下一条新闻,导致两条新闻出现了“混音”播出。央视新闻官方微博账号在21点09分发布了一条致歉微博:【致歉】今晚《新闻联播》因导播员口令失误,导致画面切换错误,特此向观众朋友表示歉意。央视特约评论员杨禹在个人微博中写道:今晚《新闻联播》出了个切换错误,@央视新闻 及时做了诚恳道歉。联播一直奉行“金标准”,压力源自全社会的高要求。其实报纸亦都有“勘误”一栏,坦诚纠错与道歉。《新闻联播》是中国影响力最大的电视新闻节目。它有不可替代的符号感,它有失误,更有悄然的进步。新的改进正在或即将发生,不妨期待");
}
File.WriteAllText(Environment.CurrentDirectory + "//1.txt", sb.ToString());
Huffman huffman = new Huffman(sb.ToString());
Stopwatch watch = Stopwatch.StartNew();
huffman.Build();
watch.Stop();
Console.WriteLine("构建赫夫曼树耗费:{0}", watch.ElapsedMilliseconds);
//将8位二进制转化为ascII码
var s = huffman.Encode();
var remain = s.Length % 8;
List<char> list = new List<char>();
var start = 0;
for (int i = 8; i < s.Length; i = i + 8)
{
list.Add((char)Convert.ToInt32(s.Substring(i - 8, 8), 2));
start = i;
}
var result = new Str编程客栈ing(list.ToArray());
//当字符编码不足8位时, 用‘艹'来标记,然后拿出'擦‘以后的所有0,1即可
result += "艹" + s.Substring(start);
File.WriteAllText(Environment.CurrentDirectory + "//2.txt", result);
Console.WriteLine("压缩完毕!");
Console.Read();
//解码
var str = File.ReadAllText(Environment.CurrentDirectory + "//2.txt");
sb.Clear();
for (int i = 0; i < str.Length; i++)
{
int ua = (int)str[i];
//说明已经取完毕了 用'艹'来做标记
if (ua == 33401)
sb.Append(str.Substring(i));
else
sb.Append(Convert.ToString(ua, 2).PadLeft(8, '0'));
}
var sss = huffman.Decode(sb.ToString());
Console.Read();
}
}
public class Huffman
{
#region 赫夫曼节点
/// <summary>
/// 赫夫曼节点
/// </summary>
public class Node
{
/// <summary>
/// 左孩子
/// </summary>
public Node left;
/// <summary>
/// 右孩子
/// </summary>
public Node right;
/// <summary>
/// 父节点
/// </summary>
public Node parent;
/// <summary>
/// 节点字符
/// </summary>
public char c;
/// <summary>
/// 节点权重
/// </summary>
public int weight;
//赫夫曼“0"or“1"
public char huffmancode;
/// <summary>
/// 标记是否为叶子节点
/// </summary>
public bool isLeaf;
}
#endregion
PriorityQueue<Node> queue = new PriorityQueue<Node>();
/// <summary>
/// 编码对应表(加速用)
/// </summary>
Dictionary<char, string> huffmanEncode = new Dictionary<char, string>();
/// <summary>
/// 解码对应表(加速用)
/// </summary>
Dictionary<string, char> huffmanDecode = new Dictionary<string, char>();
/// <summary>
/// 明文
/// </summary>
string word = string.Empty;
public Node root = new Node();
public Huffman(string str)
{
this.word = str;
Dictionary<char, int> dic = new Dictionary<char, int>();
foreach (var s in str)
{
if (dic.ContainsKey(s))
dic[s] += 1;
else
dic[s] = 1;
}
foreach (var item in dic.Keys)
{
var node = new Node()
{
c = item,
weight = dic[item]
};
//入队
queue.Eequeue(node, dic[item]);
}
}
#region 构建赫夫曼树
/// <summary>
/// 构建赫夫曼树
/// </summary>
public void Build()
{
//构建
while (queue.Count() > 0)
{
//如果只有一个节点,则说明已经到根节点了
if (queue.Count() == 1)
{
root = queue.Dequeue().t;
break;
}
//节点1
var node1 = queue.Dequeue();
//节点2
var node2 = queue.Dequeue();
//标记左孩子
node1.t.huffmancode = '0';
//标记为右孩子
node2.t.huffmancode = '1';
//判断当前节点是否为叶子节点,hufuman无度为1点节点(方便计算huffman编码)
if (node1.t.left == null)
node1.t.isLeaf = true;
if (node2.t.left == null)
node2.t.isLeaf = true;
//父节点
root = new Node();
root.left = node1.t;
root.right = node2.t;
root.weight = node1.t.weight + node2.t.weight;
//当前节点为根节点
node1.t.parent = node2.t.parent = root;
//将当前节点的父节点入队列
queue.Eequeue(root, root.weight);
}
//深度优先统计各个字符的编码
DFS(root);
}
#endregion
#region 赫夫曼编码
/// <summary>
/// 赫夫曼编码
/// </summary>
/// <returns></returns>
public string Encode()
{
StringBuilder sb = new StringBuilder();
foreach (var item in word)
{
sb.Append(huffmanEncode[item]);
}
return sb.ToString();
}
#endregion
#region 赫夫曼解码
/// <summary>
/// 赫夫曼解码
/// </summary>
/// <returns></returns>
public string Decode(string str)
{
StringBuilder decode = new StringBuilder();
string temp = string.Empty;
for (int i = 0; i < str.Length; i++)
{
temp += str[i].ToString();
//如果包含 O(N)时间
if (huffmanDecode.ContainsKey(temp))
{
decode.Append(huffmanDecode[temp]);
temp = string.Empty;
}
}
return decode.ToString();
}
#endregion
#region 深度优先遍历子节点,统计各个节点的赫夫曼编码
/// <summary>
/// 深度优先遍历子节点,统计各个节点的赫夫曼编码
/// </summary>
/// <returns></returns>
public void DFS(Node node)
{
if (node == null)
return;
//遍历左子树
DFS(node.left);
//遍历右子树
DFS(node.right);
//如果当前叶节点
if (node.isLeaf)
{
string code = string.Empty;
var temp = node;
//回溯的找父亲节点的huffmancode LgN 的时间
while (temp.parent != null)
{
//注意,这里最后形成的 “反过来的编码”
code += temp.huffmancode;
temp = temp.parent;
}
var codetemp = new String(code.Reverse().ToArray());
huffmanEncode.Add(node.c, codetemp);
huffmanDecode.Add(codetemp, node.c);
}
}
#endregion
}
}
小根堆:
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Diagnostics;
using System.Threading;
using System.IO;
namespace ConsoleApplication2
{
public class PriorityQueue<T> where T : class
{
/// <summary>
/// 定义一个数组来存放节点
/// </summary>
private List<HeapNode> nodeList = new List<HeapNode>();
#region 堆节点定义
/// <summary>
/// 堆节点定义
/// </summary>
public class HeapNode
{
/// <summary>
/// 实体数据
/// </summary>
public T t { get; set; }
/// <summary>
/// 优先级别 1-10个级别 (优先级别递增)
/// </summary>
public int level { get; set; }
public HeapNode(T t, int level)
{
this.t = t;
this.level = level;
}
public HeapNode() { }
}
#endregion
#region 添加操作
/// <summary>
/// 添加操作
/// </summary>
public void Eequeue(T t, int level = 1)
{
//将当前节点追加到堆尾
nodeList.Add(new HeapNode(t, level));
//如果只有一个节点,则不需要进行筛操作
if (nodeList.Count == 1)
return;
//获取最后一个非叶子节点
int parent = nodeList.Count / 2 - 1;
//堆调整
UpHeapAdjust(nodeList, parent);
}
#endregion
#region 对堆进行上滤操作,使得满足堆性质http://www.devze.com
/// <summary>
/// 对堆进行上滤操作,使得满足堆性质
js /// </summary>
/// <param name="nodeList"></param>
/// <param name="index">非叶子节点的之后指针(这里要注意:我们
/// 的筛操作时针对非叶节点的)
/// </param>
public void UpHeapAdjust(List<HeapNode> nodeList, int parent)
{
while (parent >= 0)
{
//当前index节点的左孩子
var left = 2 * parent + 1;
//当前index节点的右孩子
var right = left + 1;
//parent子节点中最大的孩子节点,方便于parent进行比较
//默认为left节点
var min = left;
//判断当前节点是否有右孩子
if (right < nodeList.Count)
{
//判断parent要比较的最大子节点
min = nodeList[left].level < nodeList[right].level ? left : right;
}
//如果parent节点大于它的某个子节点的话,此时筛操作
if (nodeList[parent].level > nodeList[min].level)
{
//子节点和父节点进行交换操作
var temp = nodeList[parent];
nodeList[parent] = nodeList[min];
nodeList[min] = temp;
//继续进行更上一层的过滤
parent = (int)Math.Ceiling(parent / 2d) - 1;
}
else
{
break;
}
}
}
#endregion
#region 优先队列的出队操作
/// <summary>
/// 优先队列的出队操作
/// </summary>
/// <reandroidturns></returns>
public HeapNode Dequeue()
{
if (nodeList.Count == 0)
return null;
//出队列操作,弹出数据头元素
var pop = nodeList[0];
//用尾元素填充头元素
nodeList[0] = nodeList[nodeList.Count - 1];
//删除尾节点
nodeList.RemoveAt(nodeList.Count - 1);
//然后从根节点下滤堆
DownHeapAdjust(nodeList, 0);
return pop;
}
#endregion
#region 对堆进行下滤操作,使得满足堆性质
/// <summary>
/// 对堆进行下滤操作,使得满足堆性质
/// </summary>
/// <param name="nodeList"></param>
/// <param name="index">非叶子节点的之后指针(这里要注意:我们
/// 的筛操作时针对非叶节点的)
/// </param>
public void DownHeapAdjust(List<HeapNode> nodeList, int parent)
{
while (2 * parent + 1 < nodeList.Count)
{
//当前index节点的左孩子
var left = 2 * parent + 1;
//当前index节点的右孩子
var right = left + 1;
//parent子节点中最大的孩子节点,方便于parent进行比较
//默认为left节点
var min = left;
//判断当前节点是否有右孩子
if (right < nodeList.Count)
{
//判断parent要比较的最大子节点
min = nodeList[left].level < nodeList[right].level ? left : right;
}
//如果parent节点小于它的某个子节点的话,此时筛操作
if (nodeList[parent].level > nodeList[min].level)
{
//子节点和父节点进行交换操作
var temp = nodeList[parent];
nodeList[parent] = nodeList[min];
nodeList[min] = temp;
//继续进行更下一层的过滤
parent = min;
}
else
{
break;
}
}
}
#endregion
#region 获取元素并下降到指定的level级别
/// <summary>
/// 获取元素并下降到指定的level级别
/// </summary>
/// <returns></returns>
public HeapNode GetAndDownPriority(int level)
{
if (nodeList.Count == 0)
return null;
//获取头元素
var pop = nodeList[0];
//设置指定优先级(如果为 MinValue 则为 -- 操作)
nodeList[0].level = level == int.MinValue ? --nodeList[0].level : level;
//下滤堆
DownHeapAdjust(nodeList, 0);
return nodeList[0];
}
#endregion
#region 获取元素并下降优先级
/// <summary>
/// 获取元素并下降优先级
/// </summary>
/// <returns></returns>
public HeapNode GetAndDownPriority()
{
//下降一个优先级
return GetAndDownPriority(int.MinValue);
}
#endregion
#region 返回当前优先队列中的元素个数
/// <summary>
/// 返回当前优先队列中的元素个数
/// </summary>
/// <returns></returns>
public int Count()
{
return nodeList.Count;
}
#endregion
}
}
到此这篇关于基于C#实现哈夫曼树算法的文章就介绍到这了,更多相关C#哈夫曼树算法内容请搜索编程客栈(www.devze.com)以前的文章或继续浏览下面的相关文章希望大家以后多多支持编程客栈(www.devze.com)!





 加载中,请稍侯......
加载中,请稍侯......
精彩评论