GO语言实现支持O(log(n))随机删除元素的堆
目录
- 背景
- 原理
- 数据结构
- 随机访问
- 删除
- map里面的元素index维护
- golang实现
- 数据结构
- 移除堆顶元素
- 添加元素
- 移除元素
- push()、pop()和swap()
- 另外一种实现方式
- 数据结构
- swap()、pop()、push()
- 添加元素
- 删除元素
- 重新设置值
- 时间复杂度
- 性能测试
- 总结
背景
堆是一种非常常用的数据结构,它能够支持在O(1)的时间复杂度获取到最大值(或最小值),因此我们经常在需要求最值的场景使用它。
然而普通堆它有一个缺点,它没办法快速的定位一个元素,因此它也没办法快速删除一个堆中元素,需要遍历整个堆去查询目标元素,时间复杂度是O(n),因为堆的结构在逻辑上是这样的:
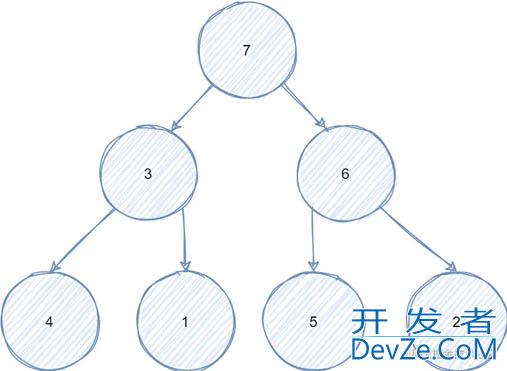
在实际实现中一般是使用一个数组来模拟:

也就是除了最大值(大顶堆)或最小值(小顶堆),其他元素其实是没有排序的,因此没办法通过二分查找的方式快速定位。
但是我们经常有一种场景,需要堆的快速求最值的性质,又需要能够支持快速的随机访问元素,特别是删除元素。
比如延迟任务的场景,我们可以使用堆对任务的到期时间戳进行排序,从而实现到期任务自动执行,但是它没办法支持随机删除一个延迟任务的需求。
下面将介绍一种支持O(log(n))随机删除元素的堆。
原理
数据结构
一种能够快速随机访问元素的数据结构是map,map如果是哈希表实现则能够在O(1)的复杂度下随机访问任何元素,而heap在知道要删除的元素的下标的情况下,也可以在O(log(n))的复杂度删除一个元素。因此我们可以结合这两个数据结构,使用map来记录heap中每个元素的下标,使用heap来获取最值。
比如对于上面的堆,我们首先给每个元素添加一个Key,这样我们才能够使用map:

然后我们使用map记录每个key对应的下标:

随机访问
这时候比如我们最简单的随机访问一个python元素C,那么就是从map[C]得到元素在heap里面的index=2,因此可以拿到元素的值。
index = m[C] // 获取元素C在heap的下标 return h[index] // 获取index在heap的值
删除
而如果我们要删除元素C,我们也是从map[C]得到元素在heap里面的index=2,然后把index为2的元素和堆最后一个元素交换,然后从index=2向上和向下调整堆,也就是:
index = m[C] // 获取元素C在heap的下标 swap(index, n - 1) // 和最后一个元素交换 pop() // 移除最后一个元素,也就是元素C down(index) // 从index向下调整堆 up(index) // 从index向上调整堆
map里面的元素index维护
上面使用的swap(i, j)和pop()操作都会影响到map里面元素的index,其实还有push(k, v)操作也会影响元素的index。
对于swap(i, j)来说需要交换两个元素的index:
h[i], h[j] = h[j], h[i] // 交换堆中两个元素 m[h[i].Key] = i // 交换map元素索引 m[h[j].Key] = j // 交换map元素索引
pop()需要删除元素的索引:
elem = h.removeLast() // 移除最后一个元素 m.remove(elem.Key) // 移除元素索引
push(k, v)需要添加元素索引:
m[key] = n // 添加元素索引 h.addLast(Entry(K, V)) // 添加元素到堆
这样其他操作就不需要维护map里面的索引问题了,保持和正常的堆的实现逻辑基本一致。
Golang实现
由于这个数据结构使用到了map和heap,因此起了一个比较短的名字叫meap,也就是m[ap]+[h]eap。
数据结构
其中主要就是一个heap和一个map,由于我们也需要从heap到map的操作,因此heap里面每个元素Entry都记录了Key,这样就可以从heap快速访问到map里面的元素,实现map里面index的修改。
LessFunc主要用于比较两个元素大小。
type Meap[K comparable, V any] struct {
h []Entry[K, V]
m map[K]int
lessFunc LessFunc[K, V]
}
type Entry[K comparable, V any] struct {
Key K
Value V
}
type LessFunc[K comparable, V any] func(e1 Entryhttp://www.devze.com[K, V], e2 Entry[K, V]) bool
移除堆顶元素
这里和正常的堆的逻辑是一样的,也就是把堆顶元素和最后一个元素交换,然后调整堆,移除堆中最后一个元素。
func (h *Meap[K, V]) Pop() Entry[K, V] {
n := h.Len() - 1
h.swap(0, n) // 堆顶和最后一个元素交换
h.down(0, n) // 调整堆
return h.pop() // 移除堆中最后一个元素
}
添加元素
这里的参数和普通的堆有一点区别,也就是我们有Key和Value,因为map必须使用一个Key,因此多了一个Key参数。
由于有map的存在,我们可以先判断元素是否已经存在,如果存在则设置Value然后调整堆即可。
如果不存在则添加元素到堆的最后,然后调整堆。
func (h *Meap[K, V]) Push(key K, value V) {
// 如果堆中已经包含这个元素
// 更新值并调整堆
if h.Contains(key) {
index := h.m[key] // 元素在堆中下标
h.h[index].Value = value // 更新堆中元素值
h.fix(index) // 向上向下调整堆
return
}
// 否则添加元素
h.push(key编程客栈, value) // 添加元素到堆的最后面
h.up(h.Len() - 1) // 向上调整堆
}
移除元素
我们首先通过key定位元素在堆中下标,然后把这个下标和堆最后一个元素交换,调整堆,最后把堆最后一个元素移除。
func (h *Meap[K, V]) Remove(key K) {
i, ok := h.m[key] // 获取元素在堆中下标
if !ok { // 如果元素不存在则直接返回
return
}
n := h.Len() - 1 // 最后一个元素索引
if n != i { // 如果被移除的元素就是堆中最后一个元素,则没必要调整了,直接移除即可
h.swap(i, n) // 和最后一个元素交换
if !h.down(i, n) { // 向下调整
h.up(i) // 向上调整
}
}
h.pop() // 移除堆中最后一个元素
}
push()、pop()和swap()
涉及到调整map中index的操作都集中到这三个操作之中:
// swap两个元素的时候
// 两个元素在map里的下标也要交换
func (h *Meap[K, V]) swap(i, j int) {
h.h[i], h.h[j] = h.h[j], h.h[i] // 交换两个元素
h.m[h.h[i].Key] = i // 更新索引
h.m[h.h[j].Key] = j // 更新索引
}
// 添加一个元素到堆的末尾
func (h *Meap[K, V]) push(key K, value V) {
h.m[key] = h.Len() // 添加索引
h.h = append(h.h, Entry[K, V]{ // 添加元素到堆尾
Key: key,
Value: value,
})
}
// 从堆的末尾移除元素
func (h *Meap[K, V]) pop() Entry[K, V] {
elem := h.h[h.Len()-1] // 堆尾元素
h.h = h.h[:h.Len()-1] // 移除堆尾元素
delete(h.m, elem.Key) // 删除堆尾元素索引
return elem
}
另外一种实现方式
其实引入一个map对性能的影响还是比较大的,有些场景我们可能不想提前引入map,是否需要map可以交给用户去决定,这时候可以使用另外一种实现方式。
这种实现方式的原理是在堆的元素Entry里面设置元素所属下标,然后把这个元素返回给用户,下标的修改和 上面的swap()、pop()、push()类似。其实原理和上面是一样的,只是把更多的控制权交给用户。
数据结构
这里Entry里面带上了index和h,index就是元素在堆里的下标,value是元素的值。这里取名叫做reap=r[emovable]+[h]eap。
type Entry[T any] struct {
value T
index int
}
func (e *Entry[T]) Value() T {
return e.value
}
type LessFunc[T any] func(e1, e2 T) bool
// reap=r[emovable]+[h]eap
// 可以通过Entry实现log(n)删除任意元素的堆
type Reap[T any] struct {
h []*Entry[T]
lessFunc LessFunc[T]
}
swap()、pop()、push()
可以看到和上面的meap是类似的,只是这里改成元素在堆的下标放到元素的index字段里面。
// swap两个元素的时候
func (h *Reap[T]) swap(i, j int) {
h.h[i], h.h[j] = h.h[j], h.h[i]
h.h[i].index = i
h.h[j].index = j
}
// 添加一个元素到堆的末尾
开发者_JAVA教程func (h *Reap[T]) push(value T) *Entry[T] {
entry := &Entry[T]{
value: value,
index: h.Len(),
}
h.h = append(h.h, entry)
return entry
}
// 从堆的末尾移除元素
func (h *Reap[T]) pop() T {
elem := h.h[h.Len()-1]
h.h = h.h[:h.Len()-1]
// 标记元素已经被删除
elem.index = -1
return elem.value
}
添加元素
添加元素到堆和普通堆一样,只是我们把Entry返回回去,这样用户才能通过Entry进行删除。
// 添加元素到堆
func (h *Reap[T]) Push(value T) *Entry[T] {
entry := h.push(value)
h.up(h.Len() - 1)
return entry
}
删除元素
这里首先判断元素是否已经被删除,这里-1是在pop()操作里面设置的。然后删除元素就是正常堆删除元素的流程。
// 移除堆里对应的元素
func (h *Reap[T]) Remove(e *Entry[T]) {
// 不能已经被删除
if e.index == -1 {
return
}
// 删除元素
i := e.index
n := h.Len() - 1
if n != i {
h.swap(i, n)
if !h.down(i, n) {
h.up(i)
}
}
h.pop()
}
重新设置值
我们还可以实现重新设置元素的值的功能,设置完新值之后,元素的优先级可能会改变,因此需要调整一下堆。
// 设置元素的值,会重新调整堆
func (h *Reap[T]) SetValue(e *Entry[T], value T) bool {
// 不能已经被删除
if e.index == -1 {
return false
}
// 重新设置值并调整
e.value = value
h.fix(e.index)
return true
}
时间复杂度
上面两种Golang实现中关键操作的时间复杂度:
| 操作 | 时间复杂度 | 描述 |
|---|---|---|
| Push() | O(log(n)) | 添加元素 |
| Pop() | O(log(n)) | 移除堆顶元素 |
| Peek() | O(1) | 获取堆顶元素 |
| Remove() | O(log(n)) | 删除元素 |
可以看到是和普通堆是一样的。
性能测试
对Heap,Reap和Meap进行简单的性能测试,也就是先全部Push()再全部Pop()。
可以看到Heap的性能是最好的,Reap比Heap差一些,主要是Reap涉及到index的维护,需要额外的数据结构和操作,而且Push()需要返回一个Entry指针给用户,因此还涉及到一次内存分配。
Meap因为引入了map,因此功能是最强大的,但是性能也是比较普通,大约只有Heap的1/6,空间消耗大约是Heap的4www.devze.com倍。
BenchmarkHeapPushAndPop-8 6042358 165.6 ns/op 41 B/op 0 allocs/op BenchmarkReapPushAndPop-8 4114232 329.6 ns/op 64 B/op 1 allocs/op BenchmarkMeapPushAndPop-8 1000000 1563 ns/op 175 B/op 0 allocs/op
总结
map的引入解决了heap无法随机删除的问题,从而能够解决更多的最值问题。而有些场景下我们本来就持有map,因此也可以使用Reap来支持随机删除,以获得更好的性能。
其实还有其他的数据结构也能够高效的解决最值问题,比如红黑树能够在O(log(n))获取最大最小值,zset也可以在O(log(n))的复杂度下获取最值,而且它们也是能够支持随机删除。当然如果你所使用的语言不支持红黑树或者zset,那么使用堆来实现也是可以的,毕竟实现一个可删除的堆比实现一个红黑树或者zset容易很多,而且堆获取最值的Peek()操作的时间复杂度是O(1)。
到此这篇关于GO语言实现支持O(log(n))随机删除元素的堆的文章就介绍到这了,更多相关GO O(javascriptlog(n))随机删除元素堆内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们!







 加载中,请稍侯......
加载中,请稍侯......
精彩评论