深入理解Pytorch中的torch. matmul()
目录
- torch.matmul()
- 语法
- 作用
- 举例
- 情形1: 一维 * 一维
- 情形2: 二维 * 二维
- 情形3: 一维 * 二维
- 情形4: 二维 * 一维
- 情形5:两个参数至少为一维且至少一个参数为 N 维(其中 N > 2),则返回批处理矩阵乘法
torch.matmul()
语法
torch.matmul(input, other, *, out=None) → Tensor
作用
两个张量的矩阵乘积
行为取决于张量的维度,如下所示:
- 如果两个张量都是一维的,则返回点积(标量)。
- 如果两个参数都是二维的,则返回矩阵-矩阵乘积。
- 如果第一个参数是一维的,第二个参数编程客栈是二维的,为了矩阵乘法的目的,在它的维数前面加上一个 1。在矩阵相乘之后,前置维度被移除。
- 如果第一个参数是二维的,第二个参数是一维的,则返回矩阵向量积。
- 如果两个参数至少为一维且至少一个参数为 N 维(其中 N > 2),则返回批处理矩阵乘法
- 如果第一个参数是一维的,则将 1 添加到其维度,以便批量矩阵相乘并在之后删除。如果第二个参数是一维的,则将 1 附加到其维度以用于批量矩阵倍数并在之后删除
- 非矩阵(即批次)维度是广播的(因此必须是可广播的)
- 例如,如果输入是( j × 1 × n × n ) (j \times 1 \times n \times n)(j×1×n×n) 张量
- 另一个是 ( k × n × n ) (k \times n \times n)(k×n×n)张量,
- out 将是一个 ( j × k × n × n ) (j \times k \times n \times n)(j×k×n×n) 张量
请注意,广播逻辑在确定输入是否可广播时仅查看批处理维度,而不是矩阵维度
例如
- 如果输入是 ( j × 1 × n × m ) (j \times 1 \times n \times m)(j×1×n×m) 张量
- 另一个是 ( k × m × p ) (k \times m \times p)(k×m×p) 张量
- 即使最后两个维度(即矩阵维度)不同,这些输入对于广播也是有效的
- out 将是一个 ( j × k × n × p ) (j \times k \times n \times p)(j×k×n×p) 张量
该运算符支持 TensorFloat32。
在某些 ROCm 设备上,当使用 float16 输入时,此模块将使用不同的向后精度

举例
情形1: 一维 * 一维
如果两个张量都是一维的,则返回点积(标量)
tensor1 = torch.Tensor([1,2,3])
tensor2 =torch.Tensor([4,5,6])
ans = torch.matmul(tensor1, tensor2)
print('tensor1 : ', tensor1)
print('tensor2 : ', tensor2)
print('ans :', ans)
print('ans.size :', ans.size())
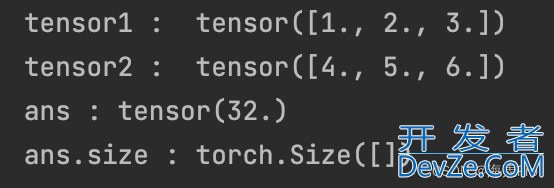
ans = 1 * 4 + 2 * 5 + 3 * 6 = 32
情形2: 二维 * 二维
如果两个参数都是二维的,则返回矩阵-矩阵乘积
也就是 正常的矩阵乘法 (m * n) * (n * k) = (m * k)
tensor1 = torch.Tensor([[1,2,3],[1,2,3]])
tensor2 =torch.Tensor([[4,5],[4,5],[4,5]])
ans = torch.matmul(tensor1, tensor2)
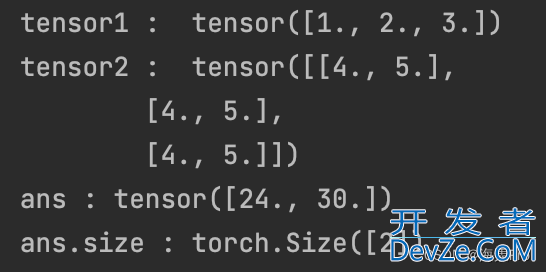
print('tensor1 : ', tensor1)
print('tensor2 : ', tensor2)
print('ans :', ans)
print('ans.size :', ans.size())

情形3: 一维 * 二维
如果第一个参数是一维的,第二个参数是二维的,为了矩阵乘法的目的,在它的维数前面加上一个 1
在矩阵相乘之后,前置维度被移除
tensor1 = torch.Tens编程or([1,2,3]) #编程 注意这里是一维
tensor2 =torch.Tensor([[4,5],[4,5],[4,5]])
ans = torch.matmul(tensor1, tensor2)
print('tensor1 : ', tensor1)
print('tensor2 : ', tensor2)
print('ans :', ans)
print('ans.size :',php ans.size())
tensor1 = torch.Tensor([1,2,3]) 修改为 tensor1 = torch.Tensor([[1,2,3]])
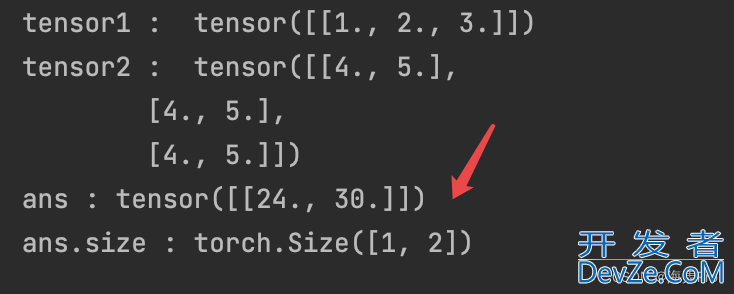
发现一个结果是[24., 30.] 一个是[[24., 30.]]
所以,当一维 * 二维时, 开始变成 1 * m(一维的维度),也就是一个二维, 再进行正常的矩阵运算,得到[[24., 30.]], 然后再去掉开始增加的一个维度,得到[24., 30.]
想象为二维 * 二维(前置维度为1),最后结果去掉一个维度即可
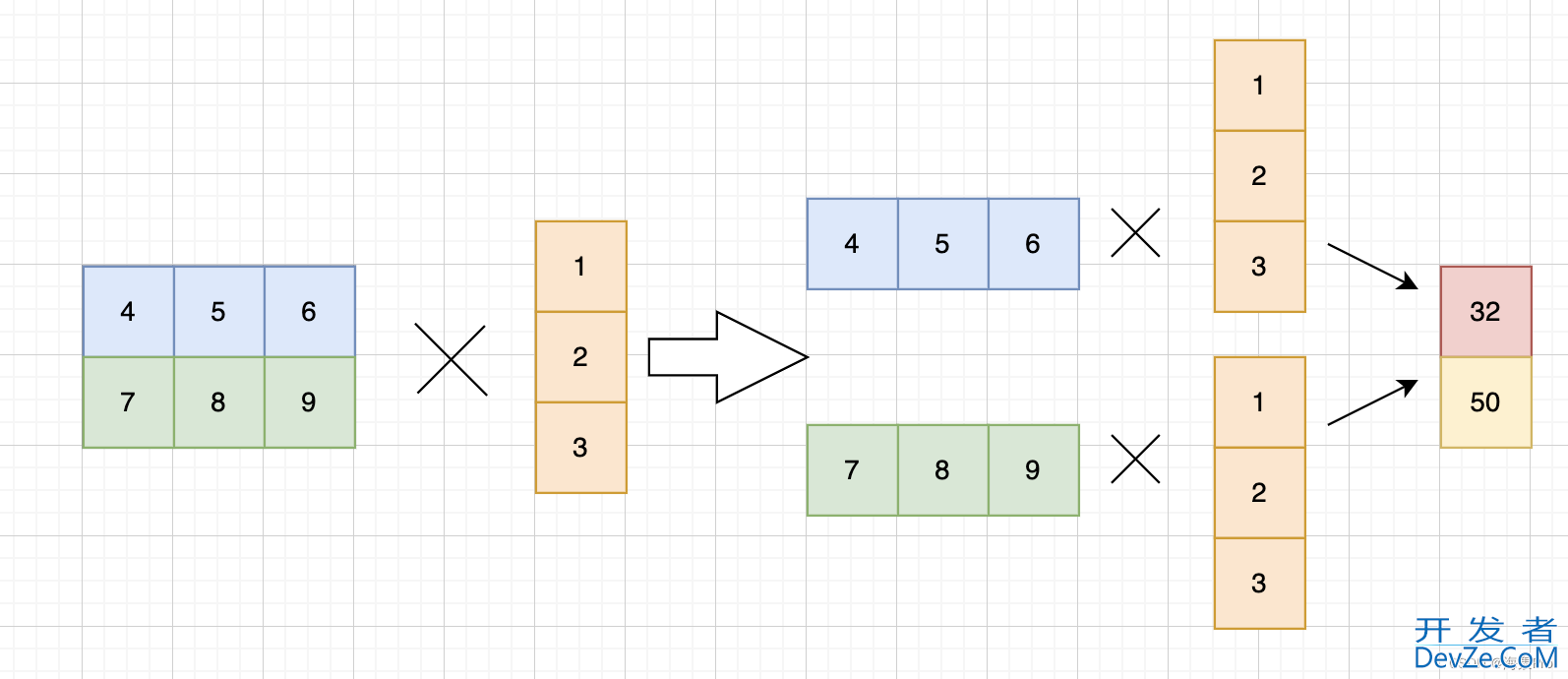
情形4: 二维 * 一维
如果第一个参数是二维的,第二个参数是一维的,则返回矩阵向量积
tensor1 =torch.Tensor([[4,5,6],[7,8,9]])
tensor2 = torch.Tensor([1,2,3])
ans = torch.matmul(tensor1, tensor2)
print('tensor1 : ', tensor1)
print('tensor2 : ', tensor2)
print('ans :', ans)
print('ans.size :', ans.size())
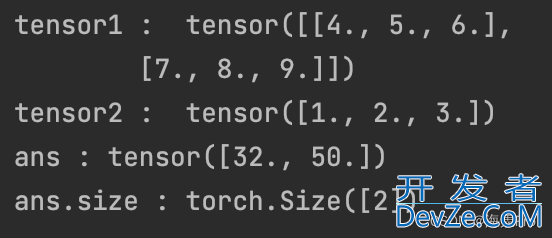
理解为:
- 把第一个二维中,想象为多个行向量
- 第二个一维想象为一个列向量
- 行向量与列向量进行矩阵乘法,得到一个标量
- 再按照行堆叠起来即可
情形5:两个参数至少为一维且至少一个参数为 N 维(其中 N > 2),则返回批处理矩阵乘法
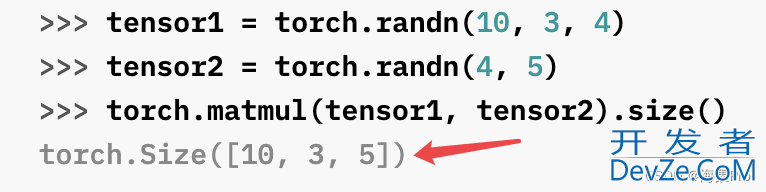
第一个参数为N维,第二个参数为一维时
ten开发者_C教程sor1 = torch.randn(10, 3, 4) tensor2 = torch.randn(4) print(torch.matmul(tensor1, tensor2).size())

(4) 先添加一个维度 (4 * 1)
得到(10 * 3 * 4) *( 4 * 1) = (10 * 3 * 1)再删除最后一个维度(添加的那个)得到结果(10 * 3)
tensor1 = torch.randn(10,2, 3, 4) # tensor2 = torch.randn(4) print(torch.matmul(tensor1, tensor2).size())

(10 * 2 * 3 * 4) * (4 android* 1) = (10 * 2 * 3) 【抵消4,删1】
第一个参数为一维,第二个参数为二维时
tensor1 = torch.randn(4) tensor2 = torch.randn(10, 4, 3) print(torch.matmul(tensor1, tensor2).size())

tensor2 中第一个10理解为批次, 10个(4 * 3)
(1 * 4)与每个(4 * 3) 相乘得到(1,3),去除1,得到(3)批次为10,得到(10,3)
tensor1 = torch.randn(4) tensor2 = torch.randn(10,2, 4, 3) print(torch.matmul(tensor1, tensor2).size())

这里批次理解为[10, 2]即可
tensor1 = torch.randn(4) tensor2 = torch.randn(10,4, 2,4,1) print(torch.matmul(tensor1, tensor2).size())

个人理解:当一个参数为一维时,它要去匹配另一个参数的最后两个维度(二维 * 二维)
比如上面的例子就是(1 * 4) 匹配 (4,1), 批次为(10,4,2)
高维 * 高维时

注:这不太好理解 … 感觉就是要找准批次,再进行乘法(靠感觉了 哈哈 离谱)
参考 https://pytorch.org/docs/stable/generated/torch.matmul.html#torch.matmul
到此这篇关于深入理解Pytorch中的torch. matmul()的文章就介绍到这了,更多相关Pytorch torch. matmul()内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们!







 加载中,请稍侯......
加载中,请稍侯......
精彩评论