开发者

Python学习之二叉树实现的示例详解

开发 作者： 逃逸的卡路里

python实现二叉树

Python学习之二叉树实现的示例详解

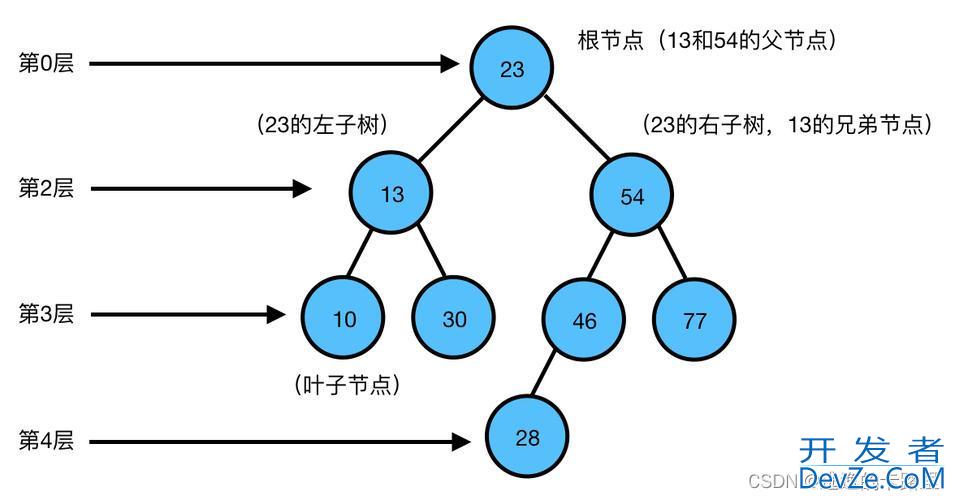
Python实现二叉树可以使用面向对象编程的方式，通过定义二叉树节点类来实现。每个节点包含一个数据元素、左右子节点指针和一些操作方法，如插入节点、查找节点、删除节点等。

以下是一个简单的二叉树实现示例：

class Node:
    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None

    def insert(self, data):
        if self.data:
            if data < self.data:
                if self.left is None:
                    self.left = Node(data)
                else:
                    self.left.insert(data)
            elif data > self.data:
                if self.right is None:
                    self.right = Node(data)
                else:
                    self.right.insert(data)
        else:
            self.data = data

    def find(self, data):
        if data < self.data:
            if self.left is None:
                return str(data) + " Not Found"
            return self.left.find(data)
        elif data > self.data:
            if self.right is None:
                return str(data) + " Not Found"
            return self.right.find(data)
        else:
            return str(self.data) + " is found"

    def inorder_traversal(self, root):
        res = []
        if root:
            res = self.inorder_traversal(root.left)
            res.append(root.data)
            res = res + self.inorder_traversal(root.right)
      编程客栈  return res

在上述代码中，Node类定义了一个节点，包含数据元素data，以及左右子节点指针left和right。insert方法用于向二叉树中插入节点，find方法用于查找二叉树中是否存在特定节点，inorder_traversal方法用于对二叉树进行python中序遍历。

下面是如何使用这个Node类来创建一个二叉树：

root = Node(50)
root.insert(30)
root.insert(20)
root.insert(40)
root.insert(70)
root.insert(60)
root.insert(80)

# 查找节点

print(root.find(70)) # Output: 70 is found
print(root.find(90)) # Output: 90 Not Found

# 中序遍历
print(root.inorder_traversal(root)) # Output: [20, 30, 40, 50, 60, 70, 80]

在上述代码中，首先创建了一个根节点root，然后使用insert方法向树中插入节点，最后使用find方法查找节点并使用inorder_traversal方法对二叉树进行中序遍历。

除了插入、查找和遍历方法，二叉树还有其他的操作方法，如删除节点、判断是否为二叉搜索树、计算树的深度等。下面是一个稍微完整一些的二叉树示例代码：

class Node:
    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None

    def insert(self, data):
        if self.data:
            if data < self.data:
                if self.left is None:
                    self.left = Node(data)
                else:
                    self.left.insert(data)
            elif data > self.data:
                if self.right is None:
                    self.right = Node(data)
                else:
                    self.right.insert(data)
        else:
            self.data = data

    def find(self, data):
        if data < self.data:
            if self.left is None:
                return None
            return self.left.find(data)
        elif data > self.data:
            if self.right is None:
                return None
  开发者_Python开发          return self.right.find(data)
        else:
            return self

    def delete(self, data):
        if self is None:
            return self

        if data < self.data:
            self.left = self.left.delete(data)
        elif data > self.data:
            self.right = self.right.delete(data)
        else:
            if self.left is None:
                temp = self.right
                self = None
                return temp
            elif self.right is androidNone:
                temp = self.left
                self = None
                return temp
            temp = self.right.minimum()
            self.data = temp.data
            self.right = self.right.delete(temp.data)
        return self

    def minimum(self):
        if self.left is None:
            return self
        return self.left.minimum()

    def is_bst(self):
        if self.left:
            if self.left.data > self.data or not self.left.is_bst():
                return False

        if self.right:
            if self.right.data < self.data or not self.right.is_bst():
                return False

        return True

    def height(self, node):
        if node is None:
            return 0

        left_height = self.height(node.left)
        right_height = self.height(node.right)

        return max(left_height, right_height) + 1

    def inorder_traversal(self, root):
        res = []
        if root:
            res = self.inorder_traversal(root.left)
            res.append(root.data)
            res = res + self.inorder_traversal(root.right)
        return res

在这个示例中，我们新增了delete方法来删除指定的节点；minimum方法来查找树中的最小节点；is_bst方法来判断当前树是否为二叉搜索树；height方法来计算树的深度。

我们可以用以下代码来测试新增的方法：

# 创建二叉树
root = Node(50)
root.insert(30)
root.insert(20)
root.insert(40)
root.insert(70)
root.insert(60)
root.insert(80)

# 删除节点
print("Deleting node 20:")
root.delete(20)
print(root.inorder_traversal(root))

# 判断是否为二叉搜索树
print("Is it a BST?:", root.is_bst())

# 计算树的深度
print("Tree height:", root.height(root))

这样我们就完成了一个比较完整的二叉树的实现，同时也演示了如何在Python中使用面向对象编程思想来实现一个数据结构。

最后附上完整的二叉树类实现代码：

class Node:
    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None

    def insert(self, data):
        if self.data:
            if data < self.data:
                if self.left is None:
                    self.left = Node(data)
                else:
                    self.left.insert(data)
            elif data > self.data:
                if self.right is None:
                    self.right = Node(data)
                else:
                    self.right.insert(data)
        else:
            self.data = data

    def find(self, data):
        if data < self.data:
            if self.left is None:
                return None
            return self.left.find(data)
        elif data > self.data:
            if self.right is None:
                return None
            return phpself.right.find(data)
        else:
            return self

    def delete(self, data):
        if self is None:
            return self

        if data < self.data:
            self.left = self.left.delete(data)
        elif data > self.data:
            self.right = self.right.delete(data)
        else:
            if编程客栈 self.left is None:
                temp = self.right
                self = None
                return temp
            elif self.right is None:
                temp = self.left
                self = None
                return temp
            temp = self.right.minimum()
            self.data = temp.data
            self.right = self.right.delete(temp.data)
        return self

    def minimum(self):
        if self.left is None:
            return self
        return self.left.minimum()

    def is_bst(self):
        if self.left:
            if self.left.data > self.data or not self.left.is_bst():
                return False

        if self.right:
            if self.right.data < self.data or not self.right.is_bst():
                return False

        return True

    def height(self, node):
        if node is None:
            return 0

        left_height = self.height(node.left)
        right_height = self.height(node.right)

        return max(left_height, right_height) + 1

    def inorder_traversal(self, root):
        res = []
        if root:
            res = self.inorder_traversal(root.left)
            res.append(root.data)
            res = res + self.inorder_traversal(root.right)
        return res

if __name__ == '__main__':
    # 创建二叉树
    root = Node(50)
    root.insert(30)
    root.insert(20)
    root.insert(40)
    root.insert(70)
    root.insert(60)
    root.insert(80)

    # 删除节点
    print("Deleting node 20:")
    root.delete(20)
    print(root.inorder_traversal(root))

    # 判断是否为二叉搜索树
    print("Is it a BST?:", root.is_bst())

    # 计算树的深度
    print("Tree height:", root.height(root))

运行代码后，可以得到以下输出：

Deleting node 20:

[30, 40, 50, 60, 70, 80]

Is it a BST?: True

Tree height: 3

这个示例包含了插入、查找、删除、遍历、判断是否为二叉搜索树和计算树的深度等。希望对看到的小伙伴有帮助。

到此这篇关于Python学习之二叉树实现的示例详解的文章就介绍到这了,更多相关Python二叉树内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！

继续阅读：Python实现二叉树

更多精彩内容

0

上一篇:

下一篇:

精彩评论

暂无评论...
登录 注册
Qedev.com
验证码 换一张
取 消

最新开发

开发排行榜

法律声明：本站内容均为网友上传，网站举办方负责审核和监督，

如存在版权或非法内容，欢迎举报，我们将尽快予以删除。

Copyright © 2018-2020 开发者. All rights reserved.

Powered by 开发者

ICP备案号： 京ICP备10032868号-9