C语言浮点型数据在内存中的存储方式详解
目录
- 前言
- 一、思考一下
- 二、浮点数存储规则
- 2.1 浮点数表示方法的规定
- 2.2 浮点数的存储
- 2.2.1 IEEE 754规定
- 2.2.2 IEEE 754对有效数字M,还有一些特别规定
- 2.2.3 IEEE 754对指数E,还有一些特别规定
- 2.2.4 实操一下看看是怎样存储的
- 2.3 浮点数从内存中取出
- 2.3.1指数E从内存中取出分三种情况
- 2.3.2 实操一下看看是怎样取出的
- 三、总结
前言
深刻了解浮点型数据在内存中的存储方式,是在修炼内功,让后续的学习更深刻,更容易发现编程过程中的问题并解决问题,继续带铁汁们学一波干货~冲!
一、思考一下
咱们先上一盘开胃菜,试试看叭
#include<stdio.h>
int main()
{
int n = 9;
float* pFloat = (float*)&n;
printf("n的值为:%d\n", n);
printf("*pFloat的值为:%f\n", *pFloat);
*pFloat = 9.0;
printf("num的值为:%d\n", n);
printf("*pFloat的值为:%f\n", *pFloat);
return 0;
}
路飞:请问打印出来都是什么结果呢?贝吉塔:简单,喏

路飞:哈哈~虽然很符合直观想法,但是错啦错啦,喏

贝吉塔:蛤??!这么奇怪的结果
二、浮点数存储规则
既然上述结果跟我们所理解的整型数据存储方式的结果不同,这就说明浮点型数据在内存中的存储方式是不一样编程客栈滴~
2.1 浮点数表示方法的规定
详细解读:
根据国际标准IEEE(电气和电子工程协会)754,任意一个二进制浮点数V可以表示成下面的形式:
(-1)^S * M * 2^E(-1)^S表示符号位。当S=0,V为正数;当S=1,V为负数M表示有效数字,大于等于1,小于22^E表示指数位
举例来说:
十进制的5.5,写成二进制是101.1,相当于(1)^0 * 1.011 * 2^2,此时
| aiphabet | Value |
|---|---|
| S | 0 |
| M | 1.011 |
| E | 2 |
此时会有铁汁有疑问,为什么5.5的二进制是101.1??不应该是101.101吗?
我们看看下图,假如是101.101,那么转换成十进制就是5.625,因为二进制每一位的权重都不同,不能想当然
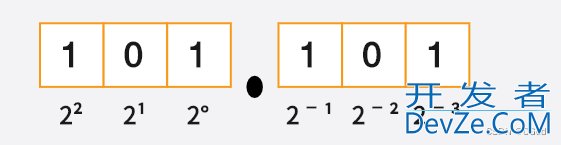
假如说给的十进制是5.3,那么这个0.3是不能精确表示的,所以说浮点数容易丢失精度
2.2 浮点数的存储
2.2.1 IEEE 754规定
对于32位的浮点数(flopythonat),最高的1位是符号位S,接着的8位是指数E,剩下的23位是有效数字M
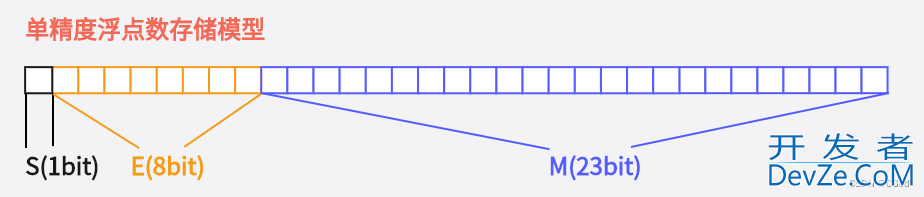
对于64位的浮点数(double),最高的1位是符号位S,接着的11位是指数E,剩下的52位是有效数字M
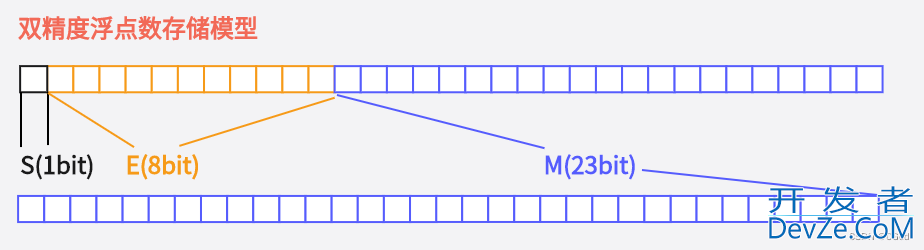
2.2.2 IEEE 754对有效数字M,还有一些特别规定
前面说过,1≤M<2,也就是说,M可以携程1.xxxxxx的形式。其中xxxxxx表示小数部分
IEEE 754规定,在计算机内部保存M时,默认这个数的第一位总是1,因此可以被舍去,只保存后面的xxxxxx。比如保存1.01时,只保存01,等到读取的时候再放回去,这样做的目的是节省空间
2.2.3 IEEE 754对指数E,还有一些特别规定
- 首先,E为一个无符号整数(unsigned int),这意味着,如果E为8位,它的取值范围为0-255;如果E为11位,它的取值范围为0-2047。
- 但是我们知道,科学计数法中的E是可以出现负数的,所以IEEE 754规定,存入内存时E的真实值必须再加上一个中间数
- 对于8位的E,中间数取127;对于11位的E,中间数取1023。
- 比如2^10的E是10,所以保存成32位浮点数时,必须保存成10+127=137,即为10001001
2.2.4 实操一下看看是怎样存储的
int main()
{
float f = 5.5f;
//(-1)^0 * 1.011 * 2^2
//S = 0
//M = 1.011
//E = 2
//这样存: 0 10000001 01100000000000000000000
//也就是: 0100 0000 1011 0000 0000 0000 0000 0000
//十六进制表示: 40 b0 00 00
return 0;
}
5.5按float存储,如图所示
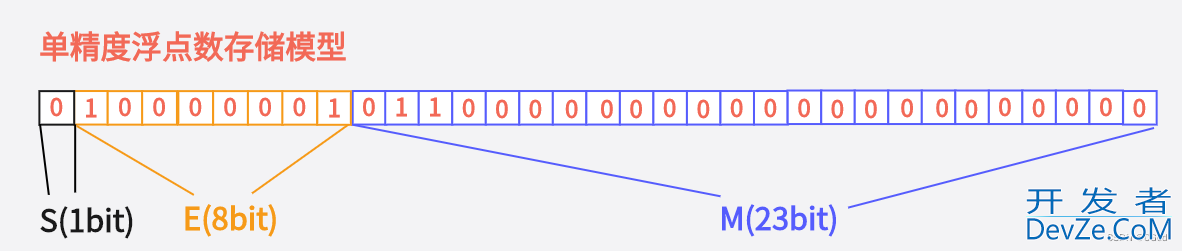
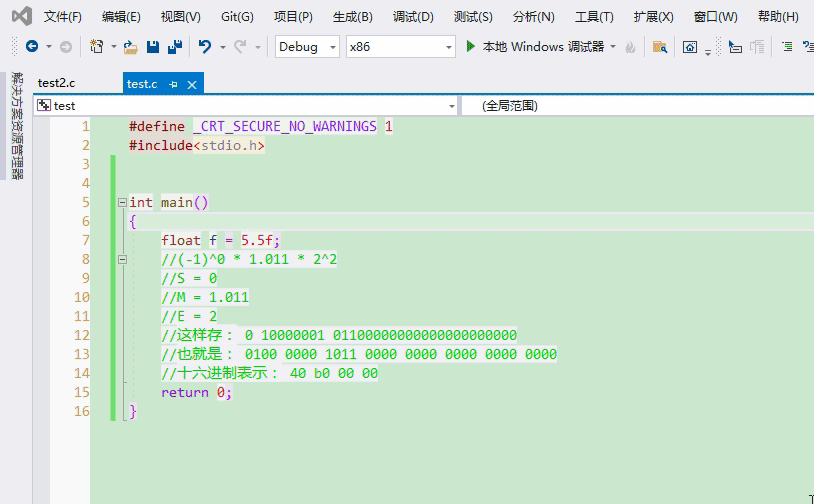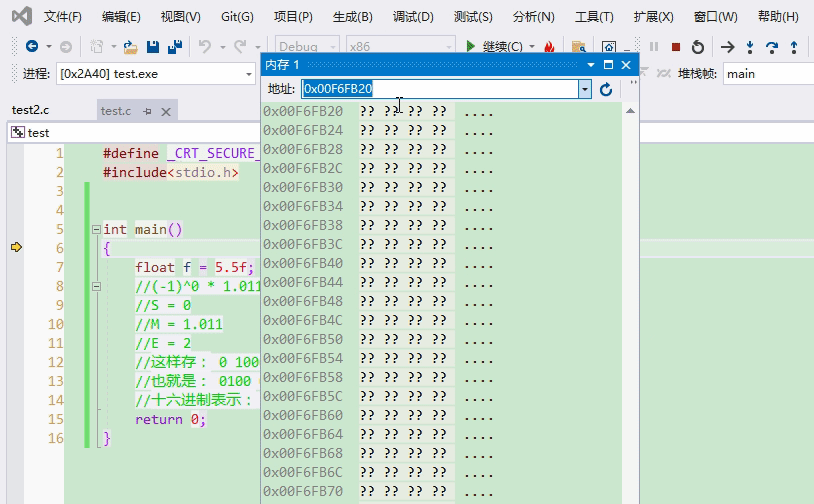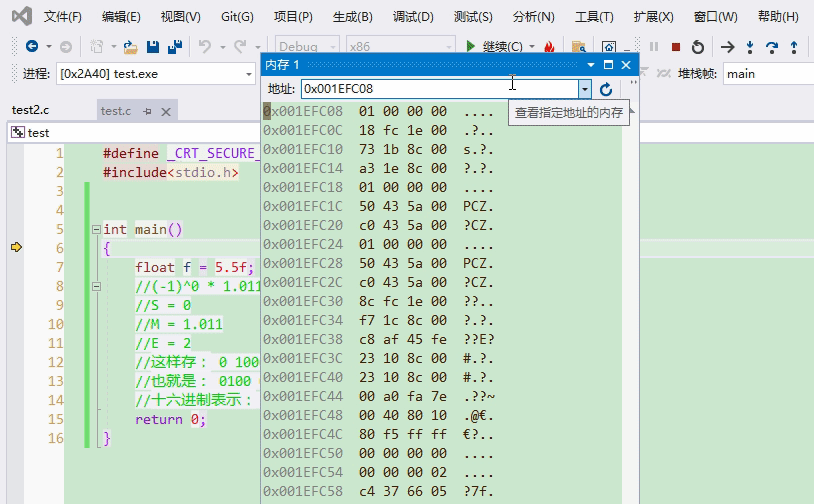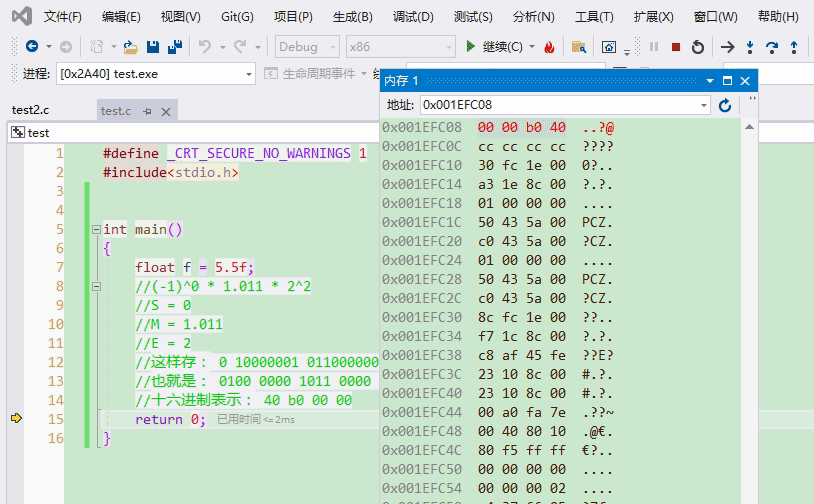
转换成十六进制就是40 b0 00 00,咱们调试看看叭~因为VS是小端字节序存储,所以地址由低到高看到的是00 00 b0 40
2.3 浮点数从内存中取出
2.3.1指数E从内存中取出分三种情况
S和M的取出很简单,原样返回,但是E我就得仔细谈谈了
- E不全为0或不全为1:
这时,把E减去之前加上去的127(或1023),得到真实值,再讲有效数字M前加上第一位的1,这种情况最简单,逆着来就是了
- E为全0:
这时真实的E为-127(或-1023),太小了,所以规定浮点数的指数E等于1-127(或1-10开发者_Python入门23)即为真实值,有效数字M不再加上第一位的1,而是还原为0.xxxxxx的小数。这样做是为了表示±0,以及接近于0的很小的数字(这是规定,大家不要纠结)
- E为全1:
这时真实的E为128,太大了,如果有效数字M全为0,表示±无穷大(正负取决于符号位S)
2.3.2 实操一下看看是怎样取出的
我们回到最开始的代码,看看能不能解决啦
#include<stdio.h>
int main()
{
int n = 9;
float* pFloat = (float*)&n;
printf("n的值为:%d\n", n);
printf("*pFloat的值为:%f\n", *pFloat);
*pFpythonloat = 9.0;
printf("num的值为:%d\n", n);
printf("*pFloat的值为:%f\n", *pFloat);
return 0;
}
答案:
- 先分析前两个输出:
首先,9是int类型的,存储按整型存储规则,就是在内存中都是以补码形式存放的,而正数的原码、反码、补码都一样
| int | 9 |
|---|---|
| 原码 | 00000000000000000000000000001001 |
| 反码 | 00000000000000000000000000001001 |
| 补码 | 00000000000000000000000000001001 |
2.第一个输出是以%d(十进制整型)输出,所以输出结果确实是9
3. 第二个输出,pFloat指针认为数据是以单精度浮点数类型存储的,所以解应用的时候也是这么做的。此时pFloat发现E全为0,按照上述规则,9取出来就变成0.000000000000000000001001 * 2^-126,即使不管后面的指数!有效数字都已经非常小android了!所以打印出来小数点后6位看到的是0.000000
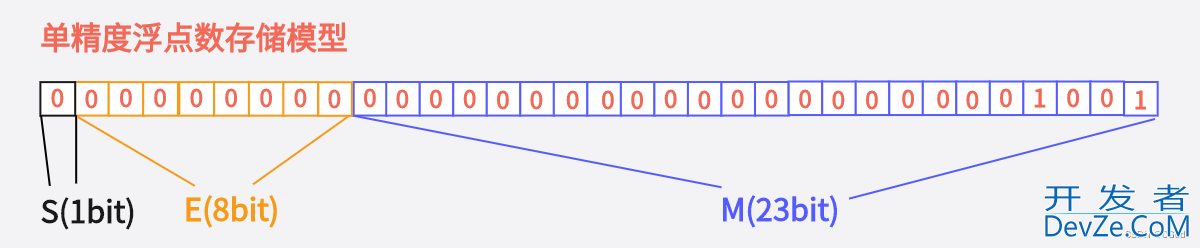
然后,分析后两个输出:
首先,9.0是float类型的,存储按浮点数存储规则,即为
(-1)^0 * 1.001 * 2^3
| float | 9.0 |
|---|---|
| S | 0 |
| M | 1.001 |
| E | 3 |
存到内存里就是:
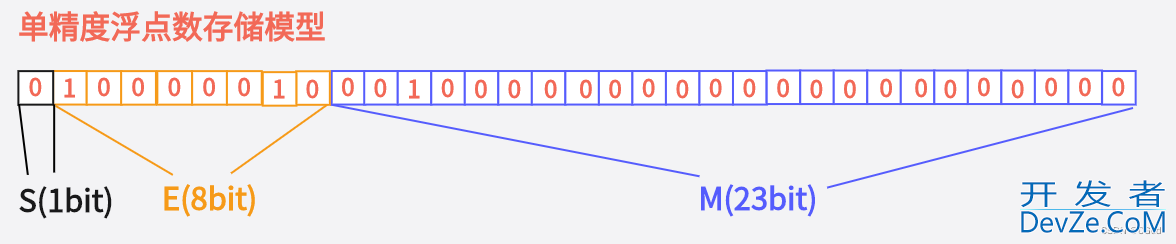
于是第三个输出,%d把它当整型输出,那么在整型眼里,直接把这32位直接转成十进制输出了,就造成了输出结果为1091567616
而第四个输出就是按float类型输出的,所以结果就是9.000000
三、总结
- 内存可以认为都是一堆同样的小格子
- 但是整型和浮点型数据在内存中的存储方式是不一样的,哪怕都是一样的内存格子,却有各自的规则限制着(看起来都是放格子里没有差别)
- 所以输出的时候,也有取出的规则,不然都一样了
到此这篇关于C语言浮点型数据在内存中的存储方式的文章就介绍到这了www.devze.com,更多相关C语言浮点型数据在内存的存储内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们!







 加载中,请稍侯......
加载中,请稍侯......
精彩评论