目录基于 brpc+etcd + 百度 AI SDK 的分布式语音识别服务实践:从代码架构到踩坑复盘一、项目背景与核心功能二、核心代码架构解析1. 整体架构概javascript览2. 关键模块代码解析三、核心问题与解决方案(踩坑复盘)1
目录当屏幕录制成了"黑屏"制造机屏幕录制的"封神"三重境界第一重境界:别把屏幕录制当"黑盒"第二重境界:屏幕录制必须"有血有肉"第三重境界:C# vs 其他方案&mda
目录为什么选择Spire.Doc for .NET进行Word转html环境准备与基础转换流程环境配置:引入Spire.Doc库Word到HTML的基础转换实践高级转换选项与常见问题处理精细化控制HTML输出:转换选项详解应对复杂Word文档:图片、表
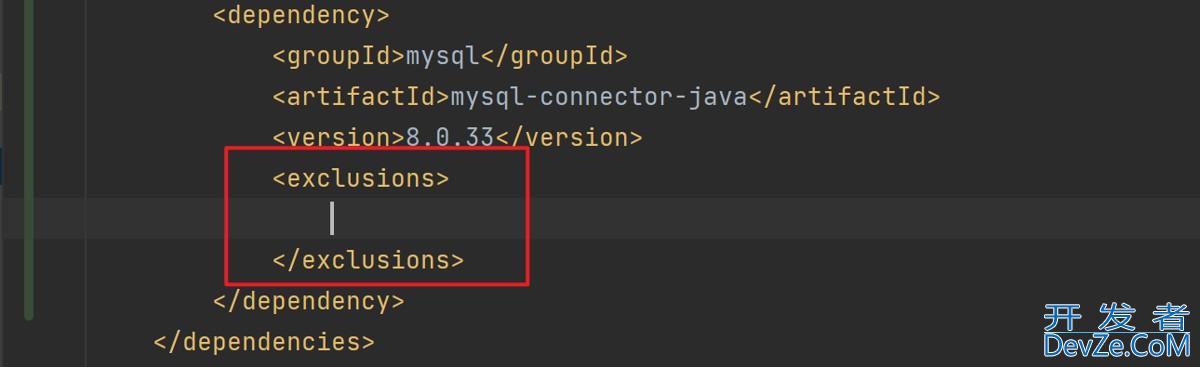
目录Maven(一)创建一个Maven项目去Maven商店下载对应的驱动包在依赖中引入本地下载的jar包(二)Maven Help 插件(三)Maven依赖管理依赖配置依赖传递依赖排除(四)Maven仓库本地仓库中央仓库编程客栈私有服务器(五)配置国
目录 Spring Boot 整合第三方组件:Redis、MyBATis、Kafka 实战 一、Spring Boot Starter 设计哲学 约定优于配置的核心思想 自动装配机制揭秘 二、Redis 整合实战 依赖配置与自动装配⚙️ Redis 配置类 Redis 操作实

目录基本知识基本思路步骤1、前端配置好tinymce富文本编辑器2、获取富文本编辑器的内容,并发送至后端3、后端在数据库创建表4、后端编写接收富文本内容的接口总结基本知识

目录问题描述解决办法总结问题描述 没有发现测试/空套件 javascript &n编程客栈bsp;

pip安装pyspark报错 python版本:Python 2.7.14 执行命令:pip install pyspark 报错 :return base64.b64encode(b).decode("ascii") MemoryError

目录游戏规则实现代码游戏规则 这是一个单人钻石棋游戏,游戏中有两种颜色的棋子:红色和绿色。每个玩家在游戏进行中轮流选择一个空格,并在该空格上放置自己的棋子。游戏的目的是尽可能地连成一条长的直线,使该直线

Sublime Text 3是一个非常好的代码编辑器。因为它的性感高亮代码配色,也因为它的体积小。但是它默认不支持GBK的编码格式,因此打开GBK代码文件,如果其中有中文的话,就会显示乱码:
精彩评论