Generating random numbers with known mean and variance
From a paper I'm reading right know:
...
S(t+1, k) = S(t, k) + ... + C*∆
...
∆ is a standard rand开发者_JAVA技巧om variable with mean 0 and variance 1.
...
How to generate this series of random values with this mean and variance? If someone has links to a C or C++ library I would be glad but I wouldn't mind implementing it myself if someone tells me how to do it :)
Do you have any restrictions on the distribution of \Delta ? if not you can just use a uniform distribution in [-sqrt(3), sqrt(3)]. The reason why this would work is because for an uniform distribution [a,b] the variance is 1/(12) (b-a)^2.
You can use the Box-Muller transform.
Suppose U1 and U2 are independent random variables that are uniformly distributed in the interval (0, 1]. Let
and
Then Z0 and Z1 are independent random variables with a normal distribution of standard deviation 1.
Waffles is a mature, stable C++ library that you can use. In particular, the noise function in the *waffles_generate* module will do what you want.
Aside from center and spread (mean and sd) also need to know the probability distribution that the random numbers are drawn from. If the paper you are reading doesn't say anything about this, and there's no other reasonable inference supported by context, then the author probably is referring to a normal distribution (gaussian)--because that's the most common, and because the two parameters one needs to completely specify a normal distribution are mean and sd. Many distributions are not specified this way--e.g., for a Gamma distribution, shape, scale, and rate are needed; to specify a Logistic, you need location and scale, etc.
If all you want it a certain mean 0 and variance 1, probably the simplest is this. Do you have a uniform random number generator unif() that gives you numbers between 0 and 1? If you want the number to be very close to a normal distribution, can just add up 12 uniform(0,1) numbers and subtract 6. If you want it to be really exactly a normal distribution, you can use the Box-Muller transform, as Mark suggested, if you don't mind throwing in a log, a sine, and a cosine.
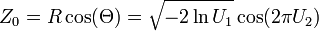
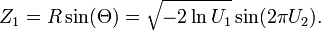
 加载中,请稍侯......
加载中,请稍侯......
精彩评论