What is the proper behaviour for a Paxos agent in this scenario?

I'm looking into Paxos and I'm confused about how the algorithm should behave in this contrived example. I hope the diagram below explains the scenario.

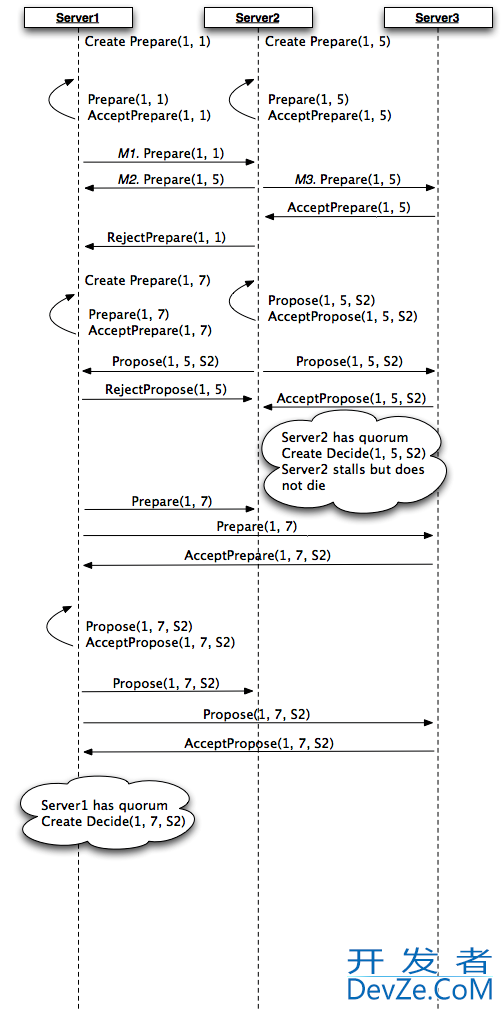
A few points:

• Each agent acts as a proposer/acceptor/learner
• Prepare messages have form (instance, proposal_num)
• Propose messages have form (instance, proposal_num, proposal_val)
• Server1 and Server2 both decide to start the proposal process at the same time
• In the beginning messages M1, M2 and M3 occur simultaneously

It seems here that although the protocol is 'correct', i.e. only one value S2 is chosen, Server1 and Server2 believe that it was chosen because of different proposal numbers.

Does the Paxos algorithm only terminate when the Decide(...) message is sent out to the learners? I must be misunderstanding Paxos Made Simple but I thought the choice was made the moment the proposers achieved quorum for their 开发者_运维知识库Propose(...) messages.

If the choice is only made after the Decide(...) message is sent out to the agents, should Server2 terminate its sending of Decide(1, 5, S2) when it recovers because it saw a later Prepare(1, 7)?

Just gonna redefine the terms (let's also throw out the 1 because we're only examining one Paxos iteration):

1) Propose(n) == propose(n), message from a proposer with current identity n

2) AcceptPrepare(n,v) == ack(n,v), message sent to proposer n. v is blank if this node hasn't accepted any value yet, o.w. v equals the value it has accepted

3) CreateDecide(n,v) == accept!(x,v), asking the nodes to accept this value from proposer with identity x. nodes will reject the message if they've ack'ed a prepare(n) message where n > x

Once quorum is achieved for prepare(n) -- that is, a majority have ack'ed the message -- then the proposer with identity n sends out a command accept!(n,v). If a prepare(n+x), x > 0, was sent out by a proposer with identity n+x -- and it's ack'ed by a majority -- between the ack(n,v) messages and the accept!(n,v), then a majority has promised not to accept values proposed with a timestamp < n+x, x > 0 (AKA the nodes will reject the accept!(n,v))

The choice is made as soon as a majority receives an accept!(n,v) message which they have not promised to ignore.

Thus, when server2 comes back online and it sends accept!(5,S2), it will be ignored because 5 < 7.

To give a counterpoint to the accepted answer, the algorithm itself never really needs to terminate in any terribly well-defined sense. It makes more sense to talk about each node individually terminating its participation in the algorithm, which is implementation-defined. Then perhaps you could say that the algorithm itself has terminated when all the participating nodes have dropped out, if that were a useful thing to want to know.

The algorithm has effectively converged as soon as a majority of acceptors have sent their AcceptPropose messages for the same ballot (in the sense that once that has happened there is no option about what value may ultimately be decided) but this is not a state of affairs that can be observed in practice: for instance if the network were to start dropping messages just before this set of AcceptPropose messages were sent, no node would be able to learn that the algorithm had converged until connectivity were restored.

However, once one node knows that the algorithm has converged (by having received AcceptPropose messages from a majority) it is safe for it to share the chosen value via conventional means, e.g. by sending a Decide message by broadcast or gossip, and for other nodes to forward it on until every node knows that convergence was achieved.

Each node can terminate its participation in the algorithm once it knows the value to which the algorithm has converged, although it may prefer to keep participating for longer, depending on your implementation constraints.

You have to think a bit about failure-tolerance to convince yourself that terminate-on-decided preserves liveness: if all the nodes that know what value was decided were to die before they could share it, would progress still be possible? The answer is, fortunately, yes: as long as a majority of nodes remains alive, if any of them knows the decided value then it can share it with the others, and if not then there's a majority of participating nodes that just need to pick a higher ballot number and run another round.

One thing to be careful of in the accepted answer is this phrase:

The choice is made as soon as a majority receives an accept!(n,v) message which they have not promised to ignore.

Firstly, there's nothing in the protocol about promising to ignore AcceptPropose messages. Promises pertain to which Propose messsages should be ignored/rejected. A majority of AcceptPropose messages can always be used to learn the chosen value, regardless of the ballot number.

Secondly, the choice is effectively made as soon as a majority sends AcceptPropose messages. You can't observe this directly so you have to wait until at least one node has received AcceptPropose messages from a majority before knowing that the choice has been made. Once that's happened, you can share the chosen value via more AcceptPropose messages or via a broadcast/gossip of Decided messages, depending on which suits your implementation constraints better.