Is Haskell truly pure (is any language that deals with input and output outside the system)?

After touching on Monads in respect to functional programming, does the feature actually make a language pure, or is it just another "get out of jail free card" for reasoning of computer systems in the real world, outside of blackboard maths?

EDIT:

This is not开发者_运维知识库 flame bait as someone has said in this post, but a genuine question that I am hoping that someone can shoot me down with and say, proof, it is pure.

Also I am looking at the question with respect to other not so pure Functional Languages and some OO languages that use good design and comparing the purity. So far in my very limited world of FP, I have still not groked the Monads purity, you will be pleased to know however I do like the idea of immutability which is far more important in the purity stakes.

---

Take the following mini-language:

data Action = Get (Char -> Action) | Put Char Action | End

Get f means: read a character c, and perform action f c.

Put c a means: write character c, and perform action a.

Here's a program that prints "xy", then asks for two letters and prints them in reverse order:

Put 'x' (Put 'y' (Get (\a -> Get (\b -> Put b (Put a End)))))

You can manipulate such programs. For example:

conditionally p = Get (\a -> if a == 'Y' then p else End)

This is has type Action -> Action - it takes a program and gives another program that asks for confirmation first. Here's another:

printString = foldr Put End

This has type String -> Action - it takes a string and returns a program that writes the string, like

Put 'h' (Put 'e' (Put 'l' (Put 'l' (Put 'o' End)))).

IO in Haskell works similarily. Although executing it requires performing side effects, you can build complex programs without executing them, in a pure way. You're computing on descriptions of programs (IO actions), and not actually performing them.

In language like C you can write a function void execute(Action a) that actually executed the program. In Haskell you specify that action by writing main = a. The compiler creates a program that executes the action, but you have no other way to execute an action (aside dirty tricks).

Obviously Get and Put are not only options, you can add many other API calls to the IO data type, like operating on files or concurrency.

Adding a result value

Now consider the following data type.

data IO a = Get (Char -> Action) | Put Char Action | End a

The previous Action type is equivalent to IO (), i.e. an IO value which always returns "unit", comparable to "void".

This type is very similar to Haskell IO, only in Haskell IO is an abstract data type (you don't have access to the definition, only to some methods).

These are IO actions which can end with some result. A value like this:

Get (\x -> if x == 'A' then Put 'B' (End 3) else End 4)

has type IO Int and is corresponding to a C program:

int f() {
  char x;
  scanf("%c", &x);
  if (x == 'A') {
    printf("B");
    return 3;
  } else return 4;
}

Evaluation and execution

There's a difference between evaluating and executing. You can evaluate any Haskell expression, and get a value; for example, evaluate 2+2 :: Int into 4 :: Int. You can execute Haskell expressions only which have type IO a. This might have side-effects; executing Put 'a' (End 3) puts the letter a to screen. If you evaluate an IO value, like this:

if 2+2 == 4 then Put 'A' (End 0) else Put 'B' (End 2)

you get:

Put 'A' (End 0)

But there are no side-effects - you only performed an evaluation, which is harmless.

How would you translate

bool comp(char x) {
  char y;
  scanf("%c", &y);
  if (x > y) {       //Character comparison
    printf(">");
    return true;
  } else {
    printf("<");
    return false;
  }
}

into an IO value?

Fix some character, say 'v'. Now comp('v') is an IO action, which compares given character to 'v'. Similarly, comp('b') is an IO action, which compares given character to 'b'. In general, comp is a function which takes a character and returns an IO action.

As a programmer in C, you might argue that comp('b') is a boolean. In C, evaluation and execution are identical (i.e they mean the same thing, or happens simultaneously). Not in Haskell. comp('b') evaluates into some IO action, which after being executed gives a boolean. (Precisely, it evaluates into code block as above, only with 'b' substituted for x.)

comp :: Char -> IO Bool
comp x = Get (\y -> if x > y then Put '>' (End True) else Put '<' (End False))

Now, comp 'b' evaluates into Get (\y -> if 'b' > y then Put '>' (End True) else Put '<' (End False)).

It also makes sense mathematically. In C, int f() is a function. For a mathematician, this doesn't make sense - a function with no arguments? The point of functions is to take arguments. A function int f() should be equivalent to int f. It isn't, because functions in C blend mathematical functions and IO actions.

First class

These IO values are first-class. Just like you can have a list of lists of tuples of integers [[(0,2),(8,3)],[(2,8)]] you can build complex values with IO.

 (Get (\x -> Put (toUpper x) (End 0)), Get (\x -> Put (toLower x) (End 0)))
   :: (IO Int, IO Int)

A tuple of IO actions: first reads a character and prints it uppercase, second reads a character and returns it lowercase.

 Get (\x -> End (Put x (End 0))) :: IO (IO Int)

An IO value, which reads a character x and ends, returning an IO value which writes x to screen.

Haskell has special functions which allow easy manipulation of IO values. For example:

 sequence :: [IO a] -> IO [a]

which takes a list of IO actions, and returns an IO action which executes them in sequence.

Monads

Monads are some combinators (like conditionally above), which allow you to write programs more structurally. There's a function that composes of type

 IO a -> (a -> IO b) -> IO b

which given IO a, and a function a -> IO b, returns a value of type IO b. If you write first argument as a C function a f() and second argument as b g(a x) it returns a program for g(f(x)). Given above definition of Action / IO, you can write that function yourself.

Notice monads are not essential to purity - you can always write programs as I did above.

Purity

The essential thing about purity is referential transparency, and distinguishing between evaluation and execution.

In Haskell, if you have f x+f x you can replace that with 2*f x. In C, f(x)+f(x) in general is not the same as 2*f(x), since f could print something on the screen, or modify x.

Thanks to purity, a compiler has much more freedom and can optimize better. It can rearrange computations, while in C it has to think if that changes meaning of the program.

---

It is important to understand that there is nothing inherently special about monads – so they definitely don’t represent a “get out of jail” card in this regard. There is no compiler (or other) magic necessary to implement or use monads, they are defined in the purely functional environment of Haskell. In particular, sdcvvc has shown how to define monads in purely functional manner, without any recourses to implementation backdoors.

---

What does it mean to reason about computer systems "outside of blackboard maths"? What kind of reasoning would that be? Dead reckoning?

Side-effects and pure functions are a matter of point of view. If we view a nominally side-effecting function as a function taking us from one state of the world to another, it's pure again.

We can make every side-effecting function pure by giving it a second argument, a world, and requiring that it pass us a new world when it is done. I don't know C++ at all anymore but say read has a signature like this:

vector<char> read(filepath_t)

In our new "pure style", we handle it like this:

pair<vector<char>, world_t> read(world_t, filepath_t)

This is in fact how every Haskell IO action works.

So now we've got a pure model of IO. Thank goodness. If we couldn't do that then maybe Lambda Calculus and Turing Machines are not equivalent formalisms and then we'd have some explaining to do. We're not quite done but the two problems left to us are easy:

• What goes in the world_t structure? A description of every grain of sand, blade of grass, broken heart and golden sunset?

• We have an informal rule that we use a world only once -- after every IO operation, we throw away the world we used with it. With all these worlds floating around, though, we are bound to get them mixed up.

The first problem is easy enough. As long as we do not allow inspection of the world, it turns out we needn't trouble ourselves about storing anything in it. We just need to ensure that a new world is not equal to any previous world (lest the compiler deviously optimize some world-producing operations away, like it sometimes does in C++). There are many ways to handle this.

As for the worlds getting mixed up, we'd like to hide the world passing inside a library so that there's no way to get at the worlds and thus no way to mix them up. Turns out, monads are a great way to hide a "side-channel" in a computation. Enter the IO monad.

Some time ago, a question like yours was asked on the Haskell mailing list and there I went in to the "side-channel" in more detail. Here's the Reddit thread (which links to my original email):

http://www.reddit.com/r/haskell/comments/8bhir/why_the_io_monad_isnt_a_dirty_hack/

---

I'm very new to functional programming, but here's how I understand it:

In haskell, you define a bunch of functions. These functions don't get executed. They might get evaluated.

There's one function in particular that gets evaluated. This is a constant function that produces a set of "actions." The actions include the evaluation of functions and performing of IO and other "real-world" stuff. You can have functions that create and pass around these actions and they will never be executed unless a function is evaluated with unsafePerformIO or they are returned by the main function.

So in short, a Haskell program is a function, composed of other functions, that returns an imperative program. The Haskell program itself is pure. Obviously, that imperative program itself can't be. Real-world computers are by definition impure.

There's a lot more to this question and a lot of it is a question of semantics (human, not programming language). Monads are also a bit more abstract than what I've described here. But I think this is a useful way of thinking about it in general.

---

I think of it like this: Programs have to do something with the outside world to be useful. What's happening (or should be happening) when you write code (in any language) is that you strive to write as much pure, side-effect-free code as possible and corral the IO into specific places.

What we have in Haskell is that you're pushed more in this direction of writing to tightly control effects. In the core and in many libraries there is an enormous amount of pure code as well. Haskell is really all about this. Monads in Haskell are useful for a lot of things. And one thing they've been used for is containment around code that deals with impurity.

This way of designing together with a language that greatly facilitates it has an overall effect of helping us to produce more reliable work, requiring less unit testing to be clear on how it behaves, and allowing more re-use through composition.

If I understand what you're saying correctly, I don't see this as a something fake or only in our minds, like a "get out of jail free card." The benefits here are very real.

---

For an expanded version of sdcwc's sort of construction of IO, one can look at the IOSpec package on Hackage: http://hackage.haskell.org/package/IOSpec

---

Is Haskell truly pure?

In the absolute sense of the term: no.

That solid-state Turing machine on which you run your programs - Haskell or otherwise - is a state-and-effect device. For any program to use all of its "features", the program will have to resort to using state and effects.

As for all the other "meanings" ascribed to that pejorative term:

To postulate a state-less model of computation on top of a machinery whose most eminent characteristic is state, seems to be an odd idea, to say the least. The gap between model and machinery is wide, and therefore costly to bridge. No hardware support feature can wash this fact aside: It remains a bad idea for practice.

This has in due time also been recognized by the protagonists of functional languages. They have introduced state (and variables) in various tricky ways. The purely functional character has thereby been compromised and sacrificed. The old terminology has become deceiving.

Niklaus Wirth

---

Does using monadic types actually make a language pure?

No. It's just one way of using types to demarcate:

• definitions that have no visible side-effects at all - values;
• definitions that potentially have visible side-effects - actions.

You could instead use uniqueness types, just like Clean does...

---

Is the use of monadic types just another "get out of jail free card" for reasoning of computer systems in the real world, outside of blackboard maths?

This question is ironic, considering the description of the IO type given in the Haskell 2010 report:

The IO type serves as a tag for operations (actions) that interact with the outside world. The IO type is abstract: no constructors are visible to the user. IO is an instance of the Monad and Functor classes.

...to borrow the parlance of another answer:

[…] IO is magical (having an implementation but no denotation) […]

Being abstract, the IO type is anything but a "get out of jail free card" - intricate models involving multiple semantics are required to account for the workings of I/O in Haskell. For more details, see:

• Tackling the Awkward Squad: … by Simon Peyton Jones;
• The semantics of fixIO by Levent Erk, John Launchbury and Andrew Moran.

---

It wasn't always like this - Haskell originally had an I/O mechanism which was at least partially-visible; the last language version to have it was Haskell 1.2. Back then, the type of main was:

main :: [Response] -> [Request]

which was usually abbreviated to:

main :: Dialogue

where:

type Dialogue = [Response] -> [Request]

and Response along with Request were humble, albeit large datatypes:

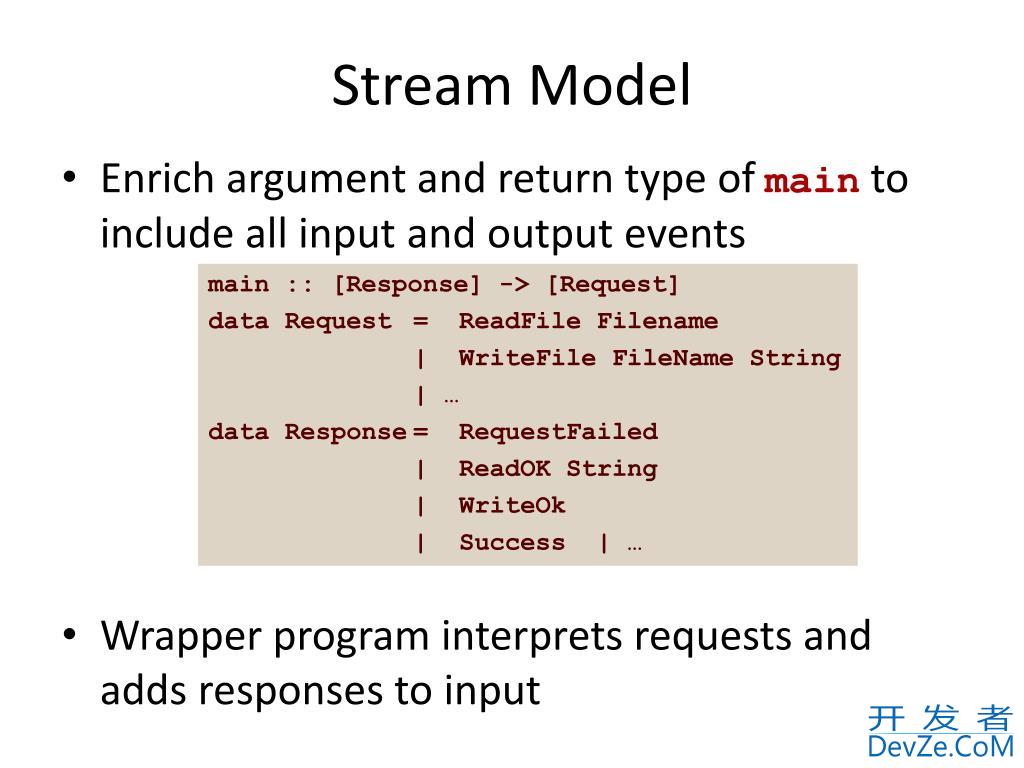
The advent of I/O using the monadic interface in Haskell changed all that - no more visible datatypes, just an abstract description. As a result, how IO, return, (>>=) etc are really defined is now specific to each implementation of Haskell.

(Why was the old I/O mechanism abandoned? "Tackling the Awkward Squad" gives an overview of its problems.)

These days, the more pertinent question should be:

• Is I/O in your implementation of Haskell referentially transparent?

As Owen Stephens notes in Approaches to Functional I/O:

I/O is not a particularly active area of research, but new approaches are still being discovered […]

The Haskell language may yet have a referentially-transparent model for I/O which doesn't attract so much controversy...

---

No, it isn't. IO monad is impure because it has side effects and mutable state (the race conditions are possible in Haskell programs so ? eh ... pure FP language don't know something like "race condition"). Really pure FP is Clean with uniqueness typing, or Elm with FRP (functional reactive programing) not Haskell. Haskell is one big lie.

Proof :

import Control.Concurrent 
import System.IO as IO
import Data.IORef as IOR

import Control.Monad.STM
import Control.Concurrent.STM.TVar

limit = 150000
threadsCount = 50

-- Don't talk about purity in Haskell when we have race conditions 
-- in unlocked memory ... PURE language don't need LOCKING because
-- there isn't any mutable state or another side effects !!

main = do
    hSetBuffering stdout NoBuffering
    putStr "Lock counter? : "
    a <- getLine
    if a == "y" || a == "yes" || a == "Yes" || a == "Y"
    then withLocking
    else noLocking

noLocking = do
    counter <- newIORef 0
    let doWork = 
        mapM_ (\_ -> IOR.modifyIORef counter (\x -> x + 1)) [1..limit]
    threads <- mapM (\_ -> forkIO doWork) [1..threadsCount]
    -- Sorry, it's dirty but time is expensive ...
    threadDelay (15 * 1000 * 1000)
    val <- IOR.readIORef counter
    IO.putStrLn ("It may be " ++ show (threadsCount * limit) ++ 
        " but it is " ++ show val) 

withLocking = do
    counter <- atomically (newTVar 0)
    let doWork = 
        mapM_ (\_ -> atomically $ modifyTVar counter (\x -> 
            x + 1)) [1..limit]
    threads <- mapM (\_ -> forkIO doWork) [1..threadsCount]
    threadDelay (15 * 1000 * 1000)
    val <- atomically $ readTVar counter
    IO.putStrLn ("It may be " ++ show (threadsCount * limit) ++ 
        " but it is " ++ show val)