How to calculate Mahalanobis distance between two time series of equal dimensions?

I am doing some data-mining on time series data. I need to calculate the distance or开发者_如何学运维 similarity between two series of equal dimensions. I was suggested to use Euclidean distance, Cos Similarity or Mahalanobis distance. The first two didn't give any useful information. I cannot seem to understand the various tutorials on the web.

So,

Given two vectors A(a1, a2, a3,...,an) and B(b1, b2, b3,...,bn) how do you find the Mahalanobis distance between them?

(I received advice on using these distance measures on SO itself, and there is a question on how to calculate Cos similarity; so please consider before closing this question)

You should estimate the covariance matrix.

The related articles in Wikipedia are this and this.

For multivariate vectors (n observations of a p-dimensional variable), the formula for the Mahalanobis distance is

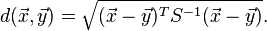
Where the S is the inverse of the covariance matrix, which can be estimated as:

where

Be careful that using the Mahalanobis distance between your vectors make sense only if all your vectors expected values are the same.

I always thought that the Mahalanobis distance is only used to classify data and detect outliers, such as discarding experimental data (sort of true/false tests). Never heard of using it as an "analogical" distance.

HTH!