How to find a random point in a quadrangle?
I have to be able to set a random location for a waypoint for a flight sim. The maths challenge is straightforward:
"To find a single random location within a quadrangle, where there's an equal chance of the point being at any location."
Visually like this:
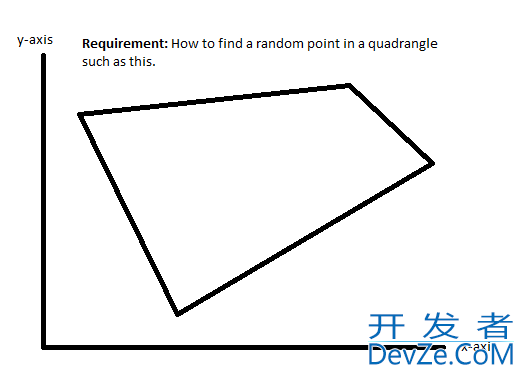
An example ABCD quadrangle is: A:[21417.78 37105.97] B:[38197.32 24009.74] C:[1364.19 2455.54] D:[1227.77 37378.81]
Thanks in advance for any开发者_如何学C help you can provide. :-)
EDIT Thanks all for your replies. I'll be taking a look at this at the weekend and will award the accepted answer then. BTW I should have mentioned that the quadrangle can be CONVEX OR CONCAVE. Sry 'bout dat.
Split your quadrangle into two triangles and then use this excellent SO answer to quickly find a random point in one of them.
Update:
Borrowing this great link from Akusete on picking a random point in a triangle.

(from MathWorld - A Wolfram Web Resource: wolfram.com)
Given a triangle with one vertex at the origin and the others at positions v1 and v2, pick
(from MathWorld - A Wolfram Web Resource: wolfram.com)
where A1 and A2 are uniform variates in the interval [0,1] , which gives points uniformly distributed in a quadrilateral (left figure). The points not in the triangle interior can then either be discarded, or transformed into the corresponding point inside the triangle (right figure).
I believe there are two suitable ways to solve this problem.
The first mentioned by other posters is to find the smallest bounding box that encloses the rectangle, then generate points in that box until you find a point which lies inside the rectangle.
Find Bounding box (x,y,width, height)
Pick Random Point x1,y1 with ranges [x to x+width] and [y to y+height]
while (x1 or y1 is no inside the quadrangle){
Select new x1,y1
}
Assuming your quadrangle area is Q and the bounding box is A, the probability that you would need to generate N pairs of points is 1-(Q/A)^N, which approaches 0 inverse exponentially.
I would reccommend the above approach, espesially in two dimensions. It is very fast to generate the points and test.
If you wanted a gaurentee of termination, then you can create an algorithm to only generate points within the quadrangle (easy) but you must ensure the probablity distribution of the points are even thoughout the quadrangle.
http://mathworld.wolfram.com/TrianglePointPicking.html
Gives a very good explination
The "brute force" approach is simply to loop through until you have a valid coordinate. In pseudocode:
left = min(pa.x, pb.x, pc.x, pd.x)
right = max(pa.x, pb.x, pc.x, pd.x)
bottom = min(pa.y, pb.y, pc.y, pd.y)
top = max(pa.y, pb.y, pc.y, pd.y)
do {
x = left + fmod(rand, right-left)
y = bottom + fmod(rand, top-bottom)
} while (!isin(x, y, pa, pb, pc, pd));
You can use a stock function pulled from the net for "isin". I realize that this isn't the fastest-executing thing in the world, but I think it'll work.
So, this time tackling how to figure out if a point is within the quad:
The four edges can be expressed as lines in y = mx + b form. Check if the point is above or below each of the four lines, and taken together you can figure out if it's inside or outside.
Are you allowed to just repeatedly try anywhere within the rectangle which bounds the quadrangle, until you get something within the quad? Might this even be faster than some fancy algorithm to ensure that you pick something within the quad?
Incidentally, in that problem statement, I think the use of the word "find" is confusing. You can't really find a random value that satisfies a condition; the randomizer just gives it to you. What you're trying to do is set parameters on the randomizer to give you values matching certain criteria.
I would divide your quadrangle into multiple figures, where each figure is a regular polygon with one side (or both sides) parallel to one of the axes. For eg, for the figure above, I would first find the maximum rectangle that fits inside the quadrangle, the rectangle has to be parallel to the X/Y axes. Then in the remaining area, I would fit triangles, such triangles will be adjacent to each side of the rectangle.
then it is simple to write a function:
1) get a figure at random. 2) find a random point in the figure.
If the figure chosen in #1 is a rectangle, it should be pretty easy to find a random point in it. The tricky part is to write a routine which can find a random point inside the triangle
You may randomly create points in a bound-in-box only stopping after you find one that it's inside your polygon.
So:
- Find the box that contains all the points of your polygon.
- Create a random point inside the bounds of the previously box found. Use random functions to generate x and y values.
- Check if that point is inside the polygon (See how here or here)
- If that point is inside the polygon stop, you're done, if not go to step 2
So, it depends on how you want your distribution.
If you want the points randomly sampled in your 2d view space, then Jacob's answer is great. If you want the points to be sort of like a perspective view (in your example image, more density in top right than bottom left), then you can use bilinear interpolation.
Bilinear interpolation is pretty easy. Generate two random numbers s and t in the range [0..1]. Then if your input points are p0,p1,p2,p3 the bilinear interpolation is:
bilerp(s,t) = t*(s*p3+(1-s)*p2) + (1-t)*(s*p1+(1-s)*p0)
The main difference is whether you want your distribution to be uniform in your 2d space (Jacob's method) or uniform in parameter space.
This is an interesting problem and there's probably as really interesting answer, but in case you just want it to work, let me offer you something simple.
Here's the algorithm:
- Pick a random point that is within the rectangle that bounds the quadrangle.
- If it is not within the quadrangle (or whatever shape), repeat.
- Profit!
edit
I updated the first step to mention the bounding box, per Bart K.'s suggestion.
 加载中,请稍侯......
加载中,请稍侯......
精彩评论