Math behind Bump(ing)?

I was randomly looking at the FA开发者_开发技巧Q for bu.mp (http://bu.mp/faq), and this part caught my eye:

Q: No way. What if somebody else bumps at the same time?

Way. We use various techniques to limit the pool of potential matches, including location information and characteristics of the bump event. If you are bumping in a particularly dense area (ex, at a conference), and we cannot resolve a unique match after a single bump, we'll just ask you to bump again. Our CTO has a PhD in Quantum Mechanics and can show the math behind that, but we suggest downloading Bump and trying it yourself!

Is there really any reason why there might be some non-trivial math behind bumping, or is the "Our CTO has a PhD in Quantum Mechanics and can show the math behind that" probably just a bit tongue-in-cheek? [I'm having a hard time imagining why something more complicated than looking at the location+time would be necessary, but maybe I'm just underestimating the problem or the kinds of data an iPhone could collect from a bump (e.g., some kind of tremor waveform?).]

I sincerely doubt there's any overly complex math involved. It just matches "bumps" that occur within a very short span of time in a particular area.

If there is more than one match within that particular timespan AND within that area it probably asks you to bump again.

The joke comes from:

One of the most shocking facts of quantum mechanics, first derived by Werner Heisemberg, is that operators does not always commute. There are a lot of different formulations and interpretations of this fact aka "uncertainty principle".

One of the most usual incarnations of the principle, and the historically first stated is

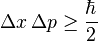
Which can be interpreted as:

"If you measure the linear momentum (mass * velocity) of something up to a great precision, you will not be able to do the same with its position"

This effect and interpretation has been object of tests, perhaps the most famous were those by Einstein (gedanken experiments) some refuted by Niels Bohr.

To be able to observe the effect, the involved mass of course should be very SMALL, so it is "visible" only for subatomic particles, never ever for something so big as an iPhone.

Similar inequalities hold for other conjugate operators, such as time and Energy.

Things are much more complicated when general relativity is taken on account (think for example in the concept of "time" .. which time?) and I think that is the idea behind the phrase "Our CTO has a PhD in Quantum Mechanics and can show the math behind".

To clarify: IF the iPhone should manifest quantum mechanics behavior, then Bump could not do the pairing (position and velocity or time and acceleration) of the phones trying to "bump"