determine if intersection of a set with conjunction of two other sets is empty

For any three given sets A, B and C: is there a w开发者_StackOverflow社区ay to determine (programmatically) whether there is an element of A that is part of the conjunction (edit: intersection) of B and C?

example:

A: all numbers greater than 3

B: all numbers lesser than 7

C: all numbers that equal 5

In this case there is an element in set A, being the number 5, that fits. I'm implementing this as specifications, so this numerical range is just an example. A, B, C could be anything.

EDIT: Thanks Niki!

It will be helpful if B.Count <= C.Count <= A.Count.

D = GetCommonElements(B,C);
if( D.Count>0 && GetCommonElements(D,A).Count >0)
{
    // what you want IS NOT EMPTY
}
else
{
    // what you want IS EMPTY
}

SET GetCommonElements(X,Y)
{
    common = {}
    for x in X:
       if Y.Contains(x):
         common.Add(x);
    return common;
}

Look at Efficient Set Intersection Algorithm.

We can use distributive laws of sets

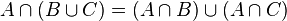
if(HasCommonElements(A,B) || HasCommonElements(A,C))
{
    // what you want IS NOT EMPTY
}
else
{
    // what you want IS EMPTY
}

bool HasCommonElements(X,Y)
{
    // if at least one common element is found return true(immediately)

    return false
}

If I'm understanding your question correctly, you want to programmatically compute the intersection of 3 sets, right? You want to see if there is an element in A that exists in the intersection of B and C, or in other words, you want to know if the intersection of A, B and C is non-empty.

Many languages have set containers and intersection algorithms so you should just be able to use those. Your example in OCaml:

module Int = struct
    type t = int
    let compare i j = if i<j then -1 else if i=j then 0 else 1
end;;

module IntSet = Set.Make(Int);;

let a = List.fold_left (fun a b -> IntSet.add b a) IntSet.empty [4;5;6;7;8;9;10];;
let b = List.fold_left (fun a b -> IntSet.add b a) IntSet.empty [0;1;2;3;4;5;6];;
let c = IntSet.add 5 IntSet.empty;;

let aIbIc = IntSet.inter (IntSet.inter b c) a;;
IntSet.is_empty aIbIc;;

This outputs false, as the intersection of a b and c is non-empty (contains 5). This of course relies on the fact that the elements of the set are comparable (in the example, the function compare defines this property in the Int module).

Alternatively in C++:

#include<iostream>
#include<set>
#include<algorithm>
#include<iterator>

int main()
{
    std::set<int> A, B, C;

    for(int i=10; i>3; --i)
        A.insert(i);
    for(int i=0; i<7; ++i)
        B.insert(i);
    C.insert(5);

    std::set<int> ABC, BC;
    std::set_intersection(B.begin(), B.end(), C.begin(), C.end(), std::inserter(BC, BC.begin()));
    std::set_intersection(BC.begin(), BC.end(), A.begin(), A.end(), std::inserter(ABC, ABC.begin()));

    for(std::set<int>::iterator i = ABC.begin(); i!=ABC.end(); ++i)
    {
        std::cout << *i << " ";
    }
    std::cout << std::endl;

    return 0;
}

The question needs further clarification. First, do you want to work with symbolic sets given by a range? And secondly, is it a one time question or is it going to be repeated in some form (if yes, what are the stable parts of the question?)?

If you want to work with ranges, then you could represent these with binary trees and define union and intersection operations on these structures. Building the tree would require O(n log n) and finding the result would require O(log n). This would not pay off with only tree sets, but it would be flexible to efficiently support any combination of ranges (if that is what you thought by 'it can be anything').

On the other hand if anything means, any set of elements, then the only option is to enumerate elements. In this case building B+ trees on sets B and C will also require O(n log n) time, but here n is the number of elements, and in the first case n is the number of ranges. The later might be several orders of magnitude bigger and of course it can represent only finite number of elements.