Difference between recursion and iteration

What is the difference? Are these the same? If not, can someone please give me an example?

MW: Iteration - 1 : the action or a process of iterating or repeating: as a : a procedure in which repetition of a sequence of operations yields results successively closer to a desired result b : the repetition of a sequence of computer instructions a specified number of times or until a condition is met

Recursion - 3 : a computer programming technique involving the use of a procedure, subroutine, function, or algorithm that calls itself one or more times until a specified condition is met at which time the res开发者_运维问答t of each repetition is processed from the last one called to the first

We can distinguish (as is done in SICP) recursive and iterative procedures from recursive and iterative processes. The former are as your definition describes, where recursion is basically the same as mathematical recursion: a recursive procedure is defined in terms of itself. An iterative procedure repeats a block of code with a loop statement. A recursive process, however, is one that takes non-constant (e.g. O(n) or O(lg(n)) space) to execute, while an iterative process takes O(1) (constant) space.

For mathematical examples, the Fibonacci numbers are defined recursively:

Sigma notation is analogous to iteration:

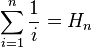
as is Pi notation. Similar to how some (mathematical) recursive formulae can be rewritten as iterative ones, some (but not all) recursive processes have iterative equivalents. All recursive procedures can be transformed into iterative ones by keeping track of partial results in your own data structure, rather than using the function call stack.

[Hurry and trump this!]

One form can be converted to the other, with one notable restriction: many "popular" languages (C/Java/normal Python) do not support TCO/TCE (tail-call-optimization/tail-call-elimination) and thus using recursion will 'add extra data to the stack' each time a method calls itself recursively.

So in C and Java, iteration is idiomatic, whereas in Scheme or Haskell, recursion is idiomatic.

As per the definitions you mentioned, these 2 are very different. In iteration, there is no self-calling, but in recursion, a function calls itself

For example. Iterative algorithm for factorial calculation

fact=1
For count=1 to n
fact=fact*count
end for

And the recursive version

function factorial(n)
if (n==1) return 1
else
n=n*factorial(n-1)
end if
end function

Generally

Recursive code is more succinct but uses a larger amount of memory. Sometimes recursion can be converted to iterations using dynamic programming.

Here's a Lisp function for finding the length of a list. It is recursive:

(defun recursive-list-length (L)
  "A recursive implementation of list-length."
  (if (null L)
      0
    (1+ (recursive-list-length (rest L)))))

It reads "the length of a list is either 0 if that list is empty, or 1 plus the length of the sub-list starting with the second element).

And this is an implementation of strlen - the C function finding the length of a nul-terminated char* string. It is iterative:

size_t strlen(const char *s)
{
    size_t n;

    n = 0;
    while (*s++)
        n++;
    return(n);
}

You goal is to repeat some operation. Using iteration, you employ an explicit loop (like the while loop in the strlen code). Using recursion, your function calls itself with (usually) a smaller argument, and so on until a boundary condition (null L in the code above) is met. This also repeats the operation, but without an explicit loop.

Recursion: Eg: Take fibonacci series for example. to get any fibonacci number we have to know the previous one. So u will berform the operation (same one) on every number lesser than the given and each of this inturn calling the same method.

fib(5) = Fib (4) + 5

fib(4) = Fib (3) + 4 . . i.e reusing the method fib

Iteration is looping like you add 1+1+1+1+1(iteratively adding) to get 5 or 3*3*3*3*3 (iteratively multiplying)to get 3^5.

For a good example of the above, consider recursive v. iterative procedures for depth-first search. It can be done using language features via recursive function calls, or in an iterative loop using a stack, but the process is inherently recursive.

For difference between recursive vs non-recursive; recursive implementations are a bit easier to verify for correctness; non- recursive implementations are a bit more efficient.

Algorithms (4th Edition)