Calculate points to create a curve or spline to draw an ellipse

I am working with Dundas maps and need to overlay the map with bubbles depicting some data. I want to add shapes to the map in order to achieve this. I can add a triangle (or any straight-line-polygon) like this:

public static void AddShape(this MapControl map, List<MapPoint> points, Color color, string name)
{
    if (points[0].X != points[points.Count - 1].X && points[0].Y != points[points.Count - 1].Y)
        points.Add(points[0]);
    var shape = new Shape
    {
        Name = name,
        BorderColor = color,
        BorderStyle = MapDashStyle.Solid,
        BorderWidth = 1,
        Color = Color.FromArgb((int)(255 * (0.3)), color)
    };
    var segments = new[] {new ShapeSegment {Type = SegmentType.Polygon, Length = points.Count}};
    shape.AddSegments(points.ToArray(), segments);
    map.Shapes.Add(shape);
}

public static void AddBermudaTriangle(this MapControl map)
{
    var points = new List<MapPoint>
                     {
                         new MapPoint(-80.15, 26.0667),
                         new MapPoint(-64.75, 32.333),
                         new MapPoint(-66.07, 18.41)
                     };
    map.AddShape(points, Color.Red, "Bermuda Triangle");
}

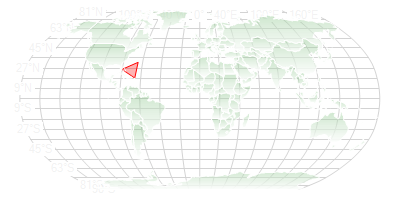
You can see that the Bermuda Triangle overlays the map in red. Now I want to calculate a set of points to pass to my AddShape method开发者_运维技巧 that would draw an elipse or circle. I just need a simple algorithm for calculating the x and y coordinates of a given number of points. Perhaps starting with a given point that would represent the centre of the circle. For example:

public static void AddCircle(this MapControl map, Point centre, double radius, string name)
{
    var points = new List<MapPoint>();
    const int n = 360;
    for(var i = 0; i < n; i++)
    {
        //calculate x & y using n, radius and centre
        double x = 0;
        double y = 0;
        points.Add(new MapPoint(x, y));
    }
    map.AddShape(points, Color.Red, name);
}

I know that the x,y calculation is simple trigonometry but I'm suffering a brain freeze. Help!

EDIT (Solved using tur!ng's code):

public static void AddCircle(this MapControl map, Color color, MapPoint centre, double radius, string name)
{
    var points = new List<MapPoint>();
    const int n = 360;
    for(var i = 0; i < n; i++)
    {
        var x = (radius * Math.Cos(i * Math.PI / 180)) + centre.X;
        var y = (radius * Math.Sin(i * Math.PI / 180)) + centre.Y;
        points.Add(new MapPoint(x, y));
    }
    map.AddShape(points, color, name);
}

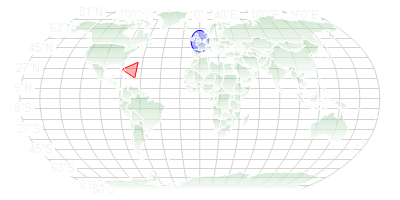
The blue circle (over Greenwich) is distorted because of the map projection over a Robinson grid.

  double x = centre.x + radius*Math.cos(2*Math.PI/360 * i);
  double y = centre.y + radius*Math.sin(2*Math.PI/360 * i);

for a circle.

Copied from an old C++ program I wrote a long time ago, it still runs at dozens of places:

  // Approximate arc with small line segments
  double sa = dp[ix].center.angle(dp[ix].co);
  double ea = dp[ix].center.angle(dp[ix+1].co);
  double r = scale * dp[ix].radius;
  double rot = ea - sa;
  double inc = rot;
  if (dp[ix].dir == ROTCW) rot = -rot;
  if (rot < 0) rot += 2*PI;
  // Compute rotation increment that generates less than 1/4 pixel error
  if (r > 2) inc = 2*acos(1-0.25/r);
  if (inc >= rot || r < 2) addPoint(x, y);
  else {
    int cnt = int(1 + rot / inc);
    inc = rot / cnt;
    if (dp[ix].dir == ROTCW) inc = -inc;
    for (int jx = 0; jx < cnt; ++jx) {
      x = offsx + scale * dp[ix].center.x + r * cos(sa);
      y = offsy + scale * dp[ix].center.y + r * sin(sa);
      addPoint(x, y);
      sa += inc;
    }
  }

acos() is the same as Math.Acos().

Recall that the formula for a circle may be expressed as

(x/r)**2 + (y/r)**2 = 1

where x and y are coordinates and r is radius.

The formula for an ellipse may be expressed as

(x/a)**2 + (y/b)**2 = 1

where a and b are the semimajor and semiminor axes (in no particular order). Choose a and b to give you an ellipse that "looks good".

You usually want to pick your points around a circle at equal angular steps, to make a better looking polygonal approximation to a true circle. For this, you use the substitutions

x = r cos theta
y = r sin theta

and run your loop for theta from zero to 2*pi. For your ellipse, you'll use

x = a cos theta
y = b sin theta

This gives you an ellipse with the semimajor and semiminor axes parallel to the X and Y axes and centered at the origin. If you want an arbitrary orientation, with an arbitrary position, you'll need to apply a rotation by an angle phi, and a translation. Any good computer graphics text will give you the necessary equations, most likely in matrix form.