Numerical computation in Java

Ok so I'm trying to use Apache Commons Math library to compute a double integral, but they are both from negative infinity (to around 1) and it's taking ages to compute. Are there any other ways of doing such operations in java? Or should it run "faster" (I mean I could actually see the result some day befor开发者_运维知识库e I die) and I'm doing something wrong?

EDIT: Ok, thanks for the answers. As for what I've been trying to compute it's the Gaussian Copula:

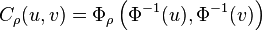
So we have a standard bivariate normal cumulative distribution function which takes as arguments two inverse standard normal cumulative distribution functions and I need integers to compute that (I know there's a Apache Commons Math function for standard normal cumulative distribution but I failed to find the inverse and bivariate versions).

EDIT2: as my friend once said "ahhh yes the beauty of Java, no matter what you want to do, someone has already done it" I found everything I needed here http://www.iro.umontreal.ca/~simardr/ssj/ very nice library for probability etc.

There are two problems with infinite integrals: convergence and value-of-convergence. That is, does the integral even converge? If so, to what value does it converge? There are integrals which are guaranteed to converge, but whose value it is not possible to determine exactly (try the integral from 1 to infinity of e^(-x^2)). If it can't be exactly returned, then an exact answer is not possible mathematically, which leaves only approximation. Apache Commons uses several different approximation schemes, but all require the use of finite bounds for correctness.

The best way to get an appropriate answer is to repeatedly evaluate finite integrals, with ever increasing bounds, and compare the results. In pseudo-code, it would look something like this:

double DELTA = 10^-6//your error threshold here
double STEP_SIZE = 10.0;
double oldValue=Double.MAX_VALUE;
double newValue=oldValue;
double lowerBound=-10; //or whatever you want to start with--for (-infinity,1), I'd
                       //start with something like -10
double upperBound=1;

do{
     oldValue = newValue;

     lowerBound-= STEP_SIZE;
     newValue = integrate(lowerBound,upperBound); //perform your integration methods here
}while(Math.abs(newValue-oldValue)>DELTA);

Eventually, if the integral converges, then you will get enough of the important stuff in that widening the bounds further will not produce meaningful information.

A word to the wise though: this kind of thing can be explosively bad if the integral doesn't converge. In that case, one of two situations can occur: Either your termination condition is never satisfied and you fall into an infinite loop, or the value of the integral oscillates indefinitely around a value, which may cause your termination condition to be incorrectly satisfied (giving incorrect results).

To avoid the first, the best way is to put in some maximum number of steps to take before returning--doing this should stop the potentially infinite loop that can result.

To avoid the second, hope it doesn't happen or prove that the integral must converge (three cheers for Calculus 2, anyone? ;-)).

To answer your question formally, no, there are no other such ways to perform your computation in java. In fact, there are no guaranteed ways of doing it in any language, with any algorithm--the mathematics just don't work out the way we want them to. However, in practice, a lot (though by no means all!) of the practical integrals do converge; its been my experience that only about ~20 iterations will give you an approximation of reasonable accuracy, and Apache should be fast enough to handle that without taking absurdly long.

Suppose you are integrating f(x) over -infinity to 1, then substitute x = 2 - 1/(1-t), and evaluate over the range 0 .. 1. Note check a maths text for how to do the substition, I'm a little rusty and its too late here.

The result of a numerical integration where one of the bounds is infinity has a good chance to be infinity as well. And it will take infinite time to prove it ;)

So you either find an equivalent formula (using real math) that can be computed or your replace the lower bound with a reasonable big negative value and look, if you can get a good estimation for the integral.

If Apache Commons Math could do numerical integration for integrals with infinite bounds in finite time, they wouldn't give it away for free ;-)

Maybe it's your algorithm.

If you're doing something naive like Simpson's rule it's likely to take a very long time.

If you're using Gaussian or log quadrature you might have better luck.

What's the function you're trying to integrate, and what's the algorithm you're using?